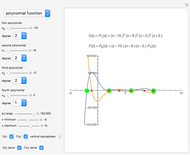
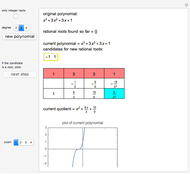
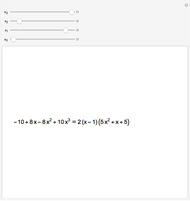
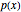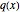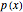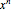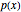If is a root of the polynomial , then 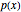can be factored as , where is a positive integer and 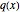is another polynomial without a root at . The number is called the degree of the root. If the roots of the polynomial are all real, the sum of the degrees of all the roots is the degree of the polynomial.

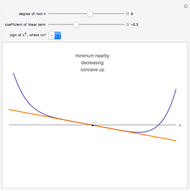
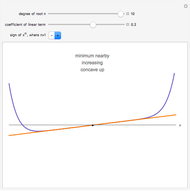
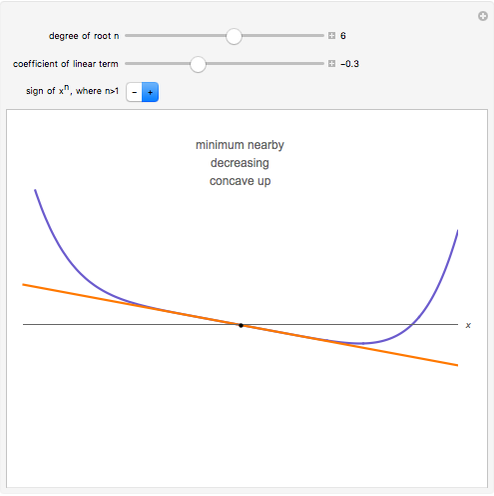
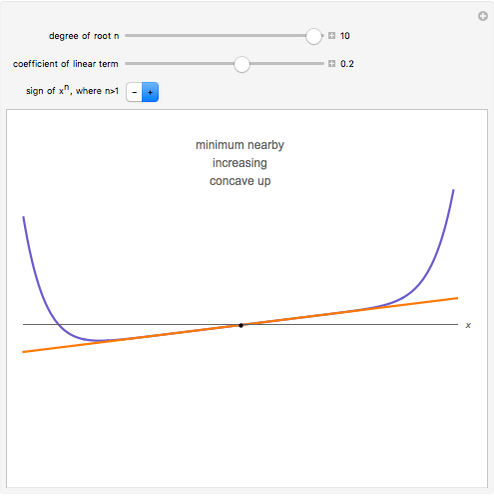
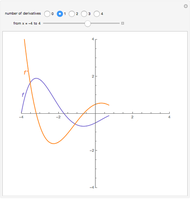
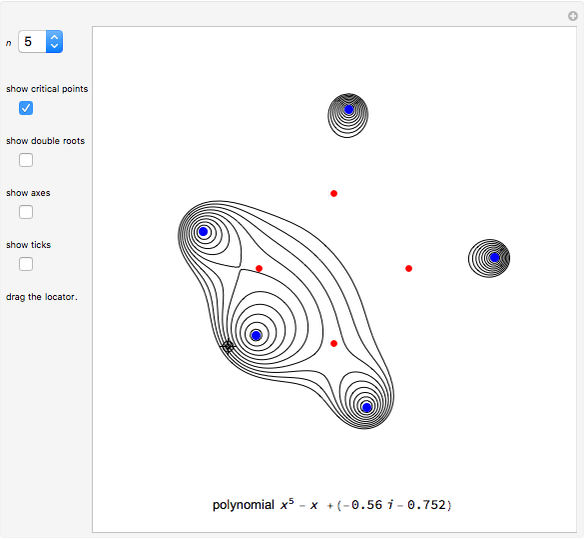
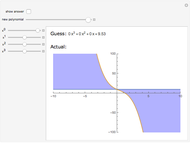
The local behavior of a polynomial 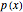at a root depends on whether the degree of the root is even or odd; the linear term of 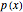is positive, zero, or negative; and the sign of its leading coefficient is positive or negative—a total of twelve possible cases.

The higher the degree, the flatter the function near the root.

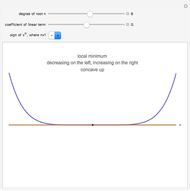
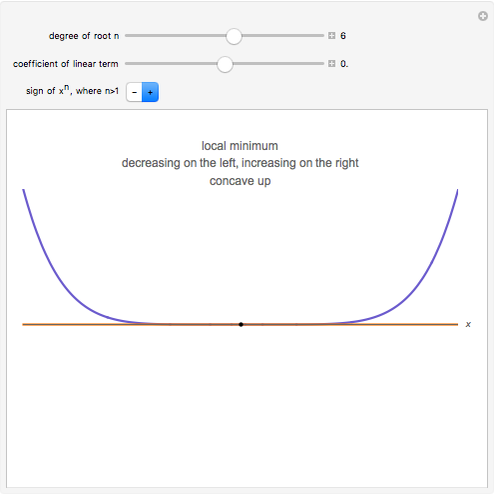
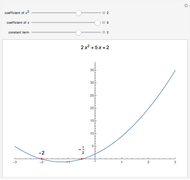
If the degree of the root is odd, there is an inflection point at the root. If the degree of the root is even, there is a maximum or minimum at or near the root.

Suppose the coefficient of the linear term is zero, so that the function has a critical point at the root. If the degree of the root is even, there is a minimum or maximum at the root, depending on whether the sign of 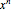is positive or negative. If the degree of the root is odd, there is a flat inflection point at the root, and the function is nondecreasing or nonincreasing near the root according to whether the sign of the leading coefficient of 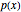is positive or negative.