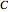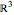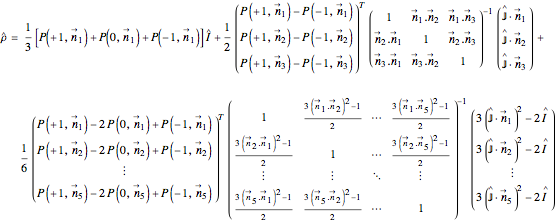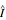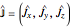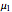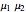Qutrit States as Probability Vectors

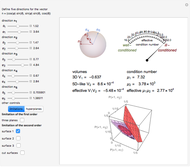
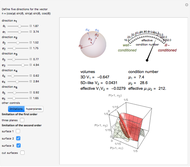
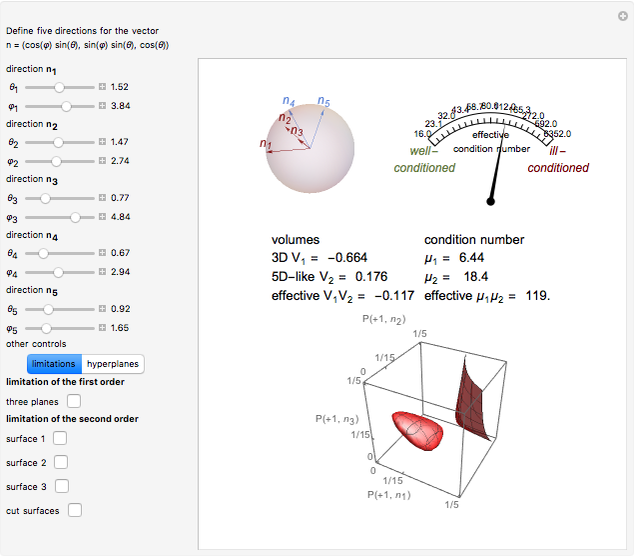
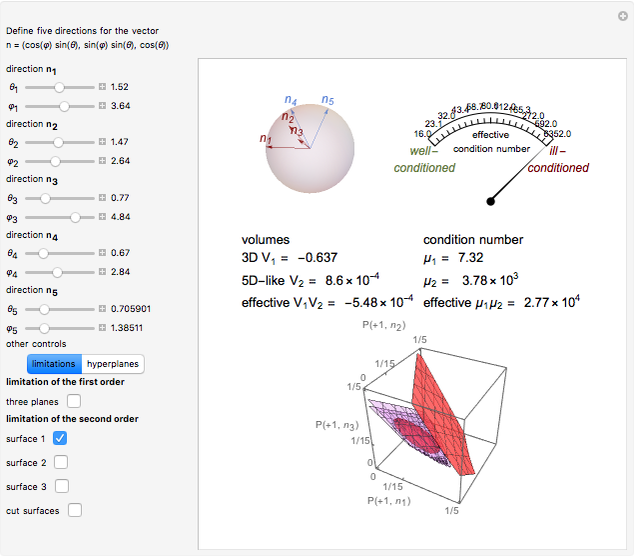
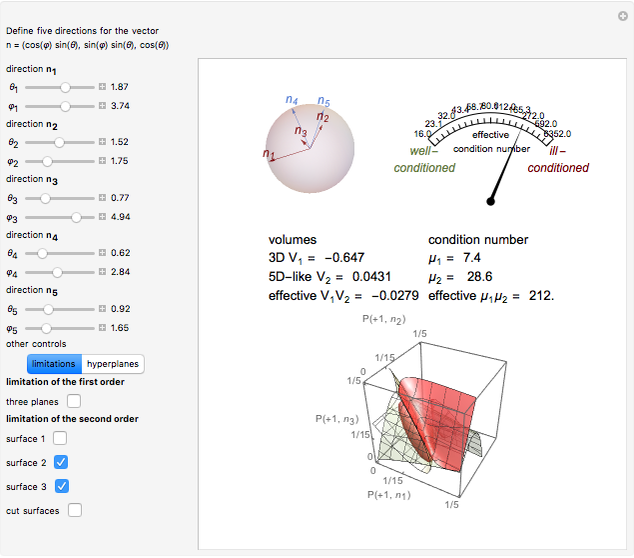
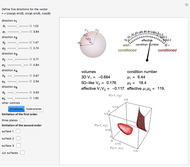
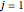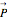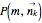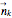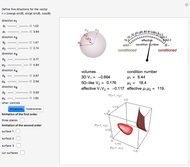
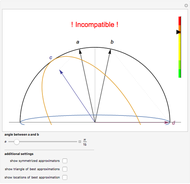
A particle with spin can represent a qutrit. Any qutrit state can be associated with a 15-dimensional probability vector whose components have definite physical meaning. The discrete variable is the spin projection and defines a direction of spin projection measurement, . The ends of the vectors 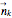lie on the unit sphere 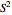, which is illustrated in the top-left corner. In general, 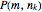is a probability distribution function of two discrete variables 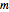and , and 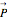determines a point on the 14-simplex. If the directions 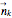are chosen with equal probability, then 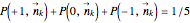for all 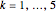. In that case, the vectors 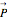can be labeled by 10 real non-negative numbers 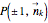, 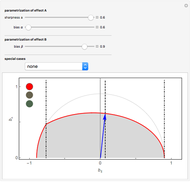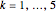. To illustrate such a probability vector we fix seven components, namely 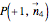, , 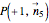and , , 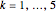that is, we determine a hyperplane that intersects the simplex, with the cut set depending on three real non-negative parameters 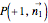, , 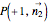and . 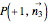The cut set is nothing else but a cube 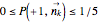, 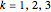. In other words, any qutrit state is associated with the probability vector of the form

,

where is a cube in of side .

The density operator is expressed through the probabilities by

where is the identity operator and are angular momentum operators.
Non-negativity of the density operator is a necessary condition leading to constraints on the probabilities . Using Sylvester's criterion, one obtains three restrictions of the first order (blue planes), three restrictions of the second order (magenta, green, and yellow surfaces), and one restriction of the third order (red surface inside the cube). In the probability space, the set of quantum states is a third-order surface located between three planes and three second-order surfaces. The set of qutrit states is illustrated at the bottom for any particular choice of directions and the cutting hyperplane.
The errors of experimentally measured probabilities result in the reconstruction procedure above being erroneous. The greater the condition numbers and of the Gram matrices above, the greater the corresponding error bar of the reconstructed density operator. (The condition number is the ratio of the absolute values of the maximum to the minimum eigenvalue.) The behavior of the condition numbers , , and the effective number is readily seen in the top-right corner of the Demonstration.