Generating Entangled Qubits

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
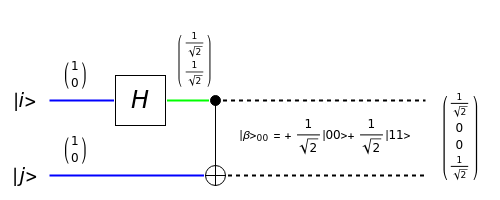
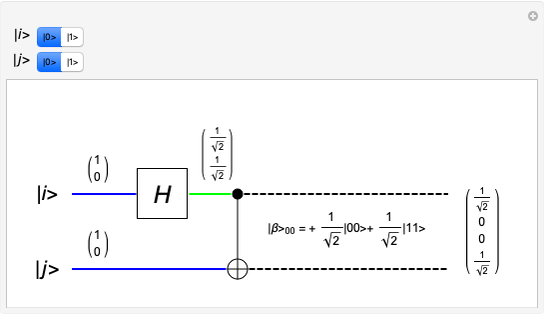
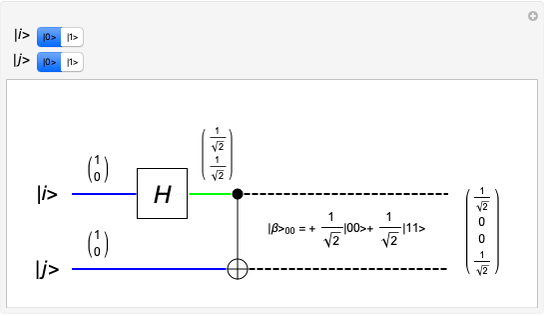
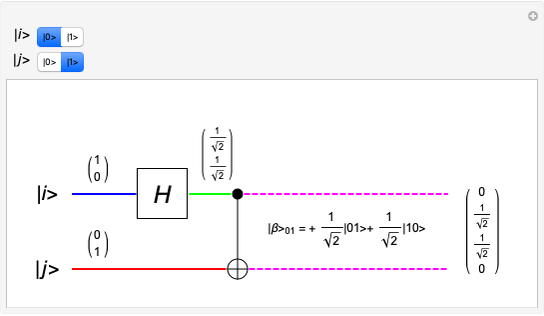
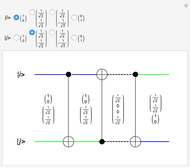
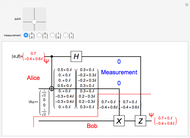
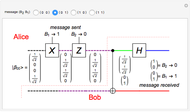
Select two input qubit states, each of which can be |0> or |1>. The quantum circuit performs a Hadamard operation on the upper qubit, and then a CNOT operation with both qubits. This yields an entangled qubit pair (an EPR pair), which makes up one of the four Bell basis states.
Contributed by: Brad Rubin (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Hadamard gate (the H box) is the 2×2 unitary matrix 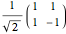 , which takes a single qubit from the upper input and produces a single qubit output. The intermediate state after the Hadamard operation is displayed. The CNOT (Controlled NOT) gate uses a control input (the solid black circle) to affect the target input (the XOR symbol). If the control input is a |0>, then the target output is the same as the target input. If the control input is a |1>, then the target output is the target input inverted. Quantum wire coloring, unique for each qubit state, lets you see the qubit state as time moves from left to right. The dashed line indicates an entangled state, and the line coloring distinguishes the different cubit states.
, which takes a single qubit from the upper input and produces a single qubit output. The intermediate state after the Hadamard operation is displayed. The CNOT (Controlled NOT) gate uses a control input (the solid black circle) to affect the target input (the XOR symbol). If the control input is a |0>, then the target output is the same as the target input. If the control input is a |1>, then the target output is the target input inverted. Quantum wire coloring, unique for each qubit state, lets you see the qubit state as time moves from left to right. The dashed line indicates an entangled state, and the line coloring distinguishes the different cubit states.
Permanent Citation