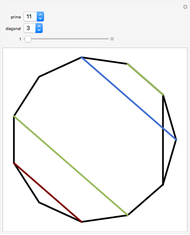
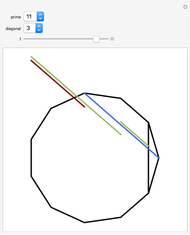
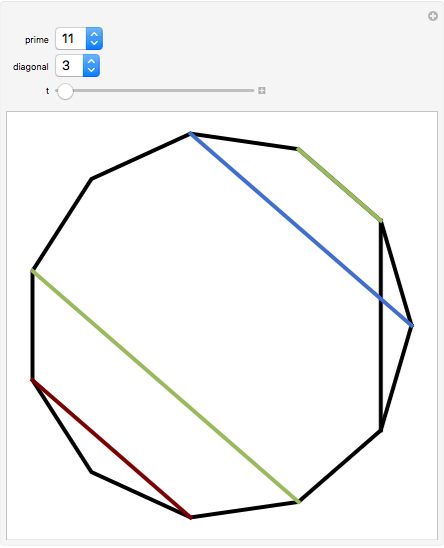
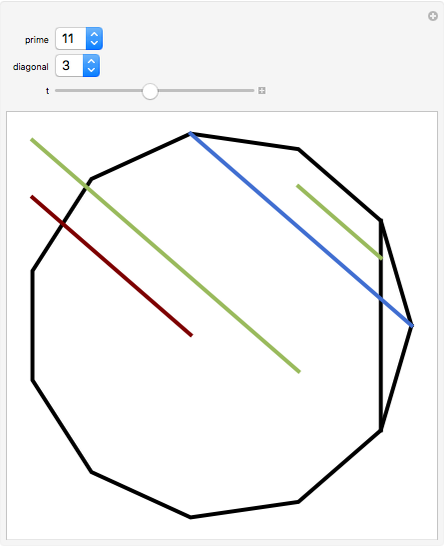
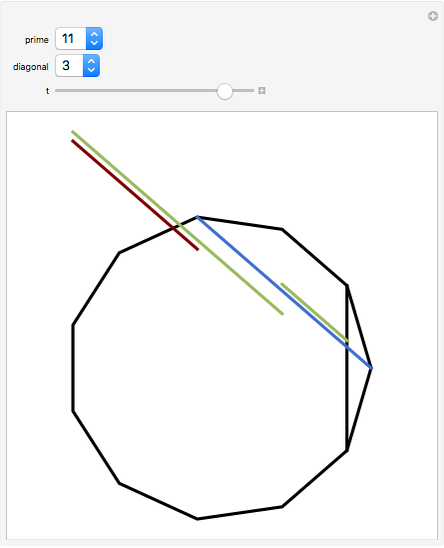
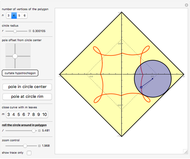
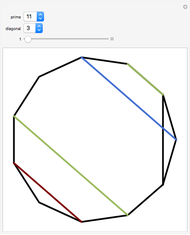
In a regular polygon of unit side, a similar triangle argument shows that the reciprocal of the length of a given diagonal (shown in blue) is the length of the portion of that diagonal to the right of the black vertical diagonal shown. If you number the diagonals in order of increasing size (including the side of the polygon as diagonal one), and if the index of the diagonal is prime to the number of sides of the polygon, the reciprocal length can be found by adding lengths of other diagonals to the original one and subtracting lengths of other diagonals from it. This is illustrated for several -gons with prime. Choose a prime, choose a diagonal, and then move the slider to see which diagonal lengths need to be added and subtracted. The total length of the blue and red diagonals is balanced by the green diagonal, except for the reciprocal portion on the right.