Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Roulette (Epitrochogon) of a Disk Rolling around a Regular Polygon

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

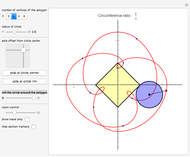
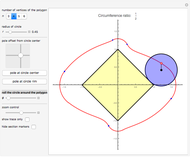
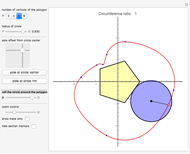
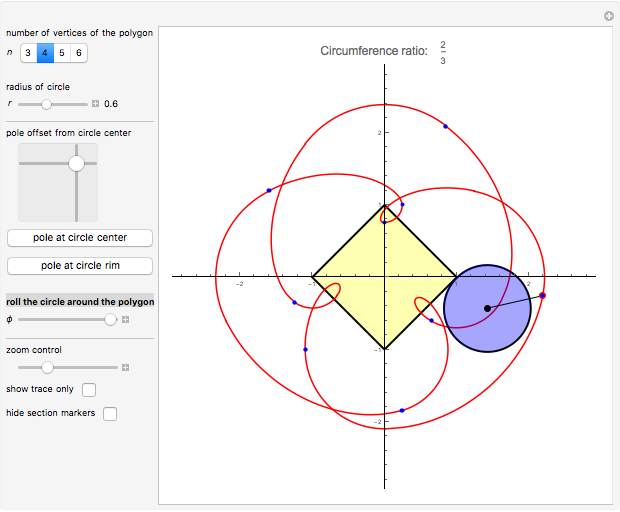
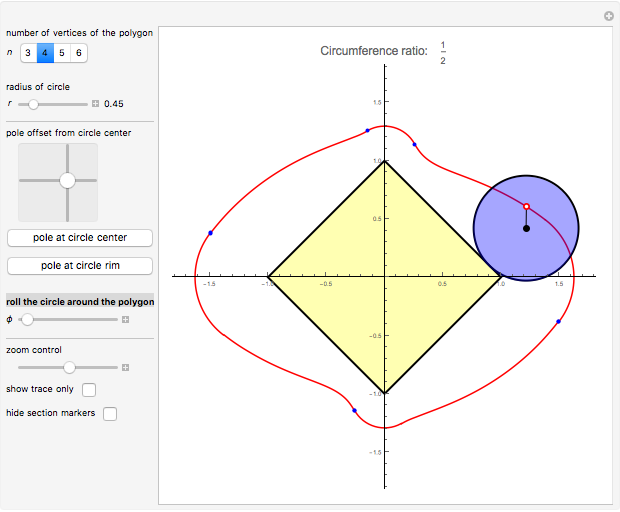
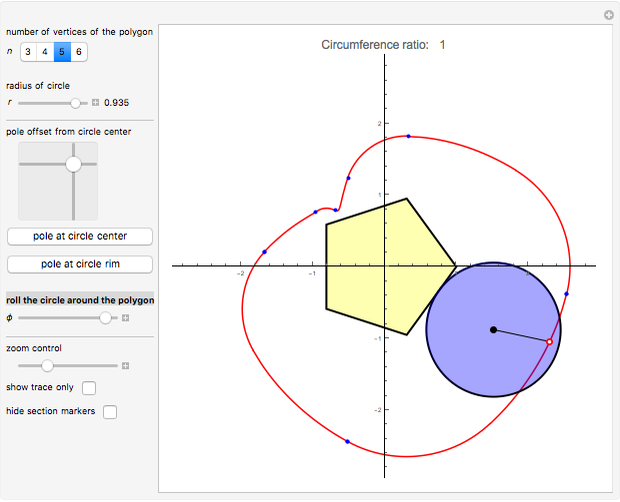
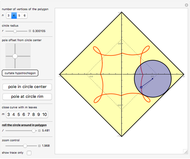
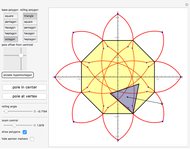
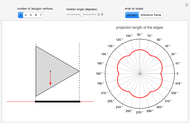
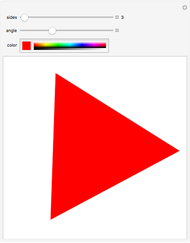
This Demonstration simulates a circle rolling without slipping on the outside of a stationary regular polygon of circumradius 1. A point is attached to the circle; its trace is called an epitrochogon.

[more]

For generalized cyclogons [1] and generalized trochoidal curves [2], these roulettes can be considered a limiting case of epitrochogons with an infinite number of vertices of the rolling polygon.

These epitrochogons consist of sequences of two distinct curve types, each generated by a different type of motion:

1. a cycloidal or rolling motion of the circle along the straight edges of the polygon.

2. a circular motion when turning around the vertices of the polygon.

[less]

Contributed by: Erik Mahieu (December 2016)
Open content licensed under CC BY-NC-SA

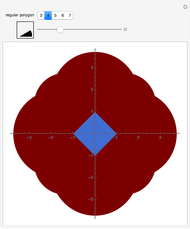
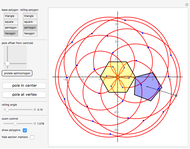
Snapshots

Details

References

[1] T. M. Apostol and M. A. Mnatsukanian, "Generalized Cyclogons," Math Horizons, 2002 pp. 25–28. www.mamikon.com/USArticles/GenCycloGons.pdf.

[2] T. M. Apostol and M. A. Mnatsukanian, "Area & Arc Length of Trochogonal Arches," Math Horizons, 2003 pp. 24–30. www.mamikon.com/USArticles/TrochoGons.pdf.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send