Recursive Partitioning for Supervised Learning

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
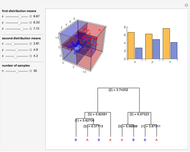
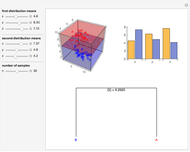
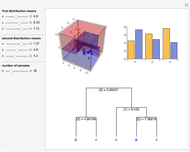
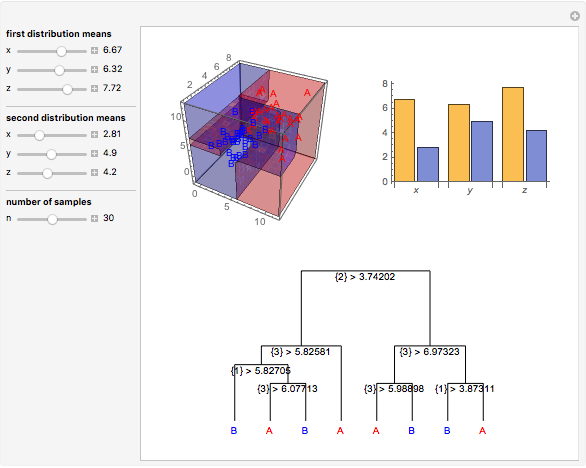
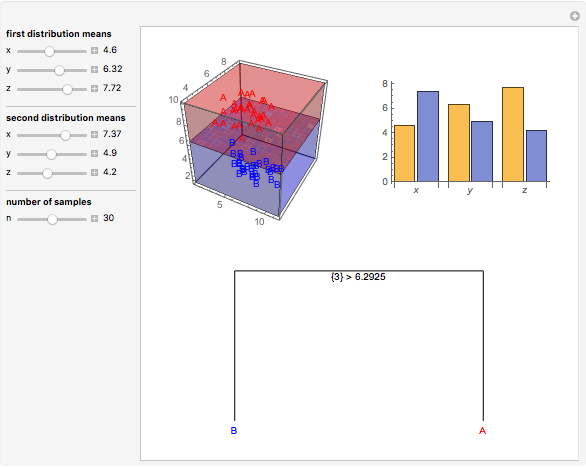
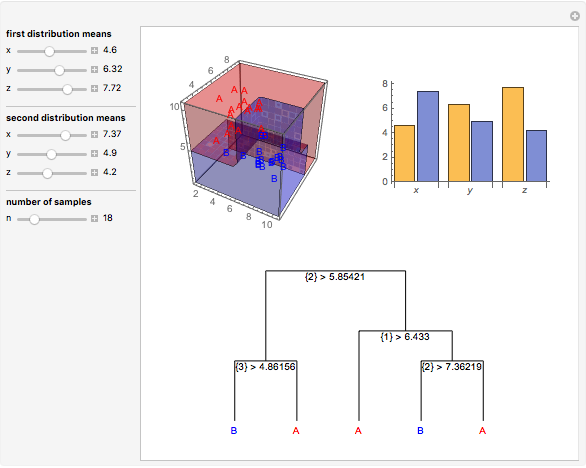
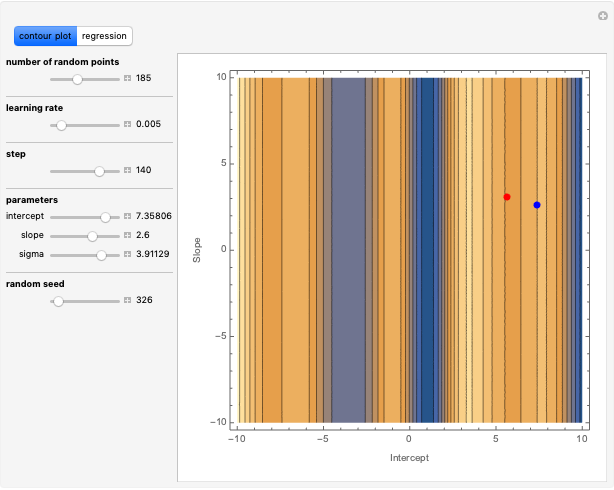
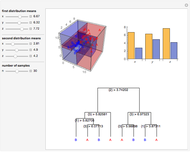
Data is sampled from two three-dimensional Gaussian distributions with means that you can vary. Data points from the first Gaussian are labeled  and data points from the second Gaussian are labeled
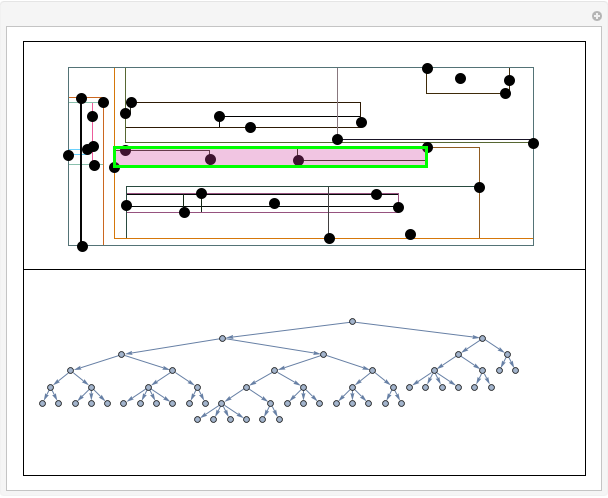
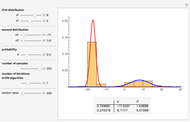
and data points from the second Gaussian are labeled 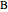 . The recursive partitioning algorithm is run on this training data to determine rules for classifying new data points. The first plot shows the training data and the regions that are determined by the algorithm. The bar chart at the top right gives a visual representation of the means of the Gaussian distributions. The tree at the bottom is a visual representation of the classification rules determined by the algorithm. Each path to a leaf node represents a region in space.
. The recursive partitioning algorithm is run on this training data to determine rules for classifying new data points. The first plot shows the training data and the regions that are determined by the algorithm. The bar chart at the top right gives a visual representation of the means of the Gaussian distributions. The tree at the bottom is a visual representation of the classification rules determined by the algorithm. Each path to a leaf node represents a region in space.
Contributed by: Anthony Fox (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Recursive partitioning is a tree-based method for classifying data. For data points in 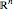 with labels
with labels 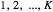 , the recursive partitioning algorithm splits the data in one of the
, the recursive partitioning algorithm splits the data in one of the  dimensions into two sets such that some node purity criterion is met. The simplest node purity criterion, called the Gini index, attempts to maximize the proportion of data points with one of the
dimensions into two sets such that some node purity criterion is met. The simplest node purity criterion, called the Gini index, attempts to maximize the proportion of data points with one of the 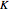 labels in each set. The partitioning algorithm is then run recursively on each set until nodes are totally pure in the sense that only one of the
labels in each set. The partitioning algorithm is then run recursively on each set until nodes are totally pure in the sense that only one of the 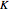 class labels is represented. Thus recursive partitioning splits the feature space into distinct regions. Each region is then given a label based on the represented class in that region.
class labels is represented. Thus recursive partitioning splits the feature space into distinct regions. Each region is then given a label based on the represented class in that region.
Recursive partitioning is a fast and fairly accurate algorithm for classifying data. It works well for real-valued variables as well as for categorical variables. It also has the appealing property of being interpretable. For instance, consider a medical example, a model for predicting whether a patient has diabetes or not. The training data consists of height, weight, age, and so on and each case is labeled either "Diabetes" or "Not". The recursive partitioning algorithm would construct a rule that maps naturally to a medical professional's intuition: If the patient's age is greater than 50 and the patient's weight is greater than 180 pounds and the patient's height is less than 5' 5", then use the label "Diabetes", and so on.
T. Hastie, R. Tibshirani, and J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed., New York: Springer, 2001.
Permanent Citation