Riemann's Theorem on Rearranging Conditionally Convergent Series

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
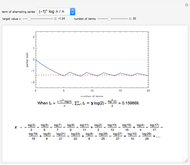
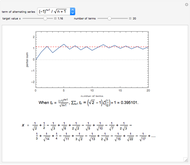
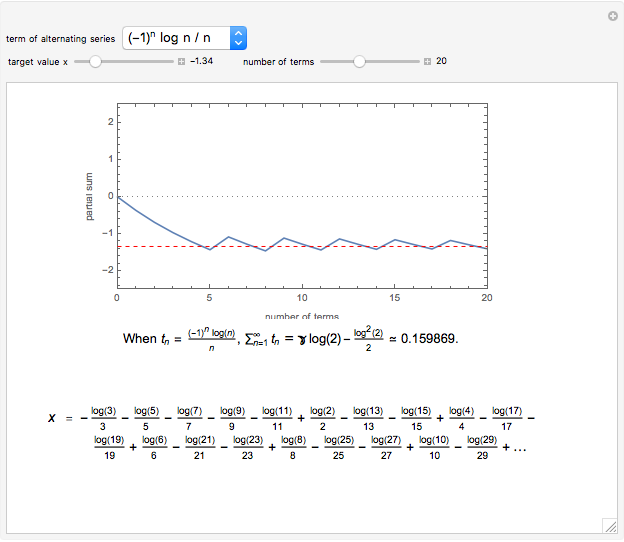
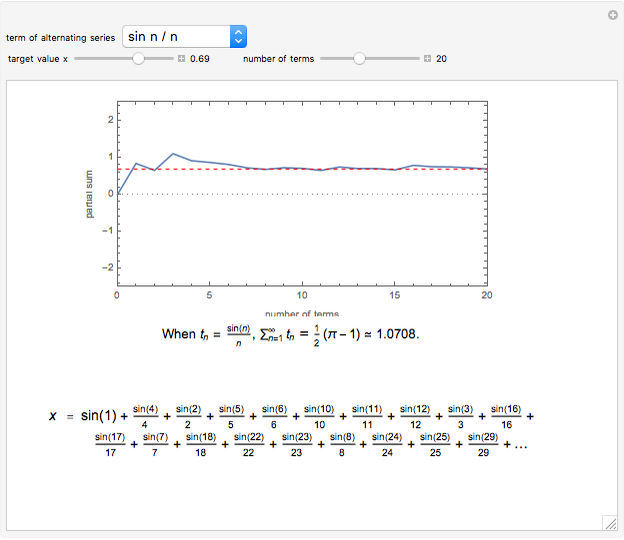
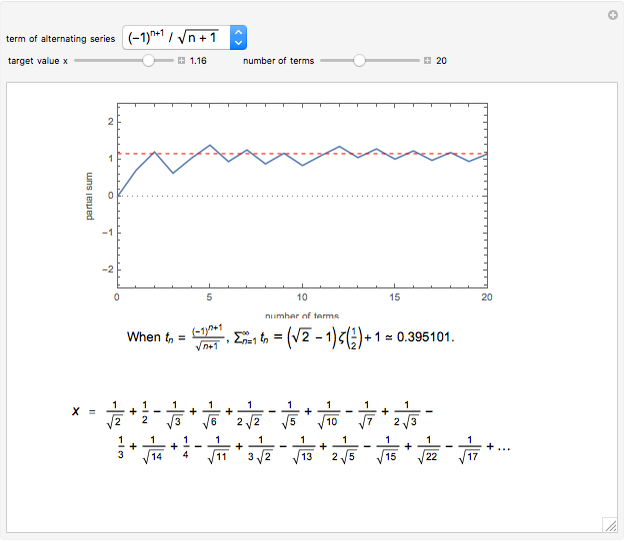
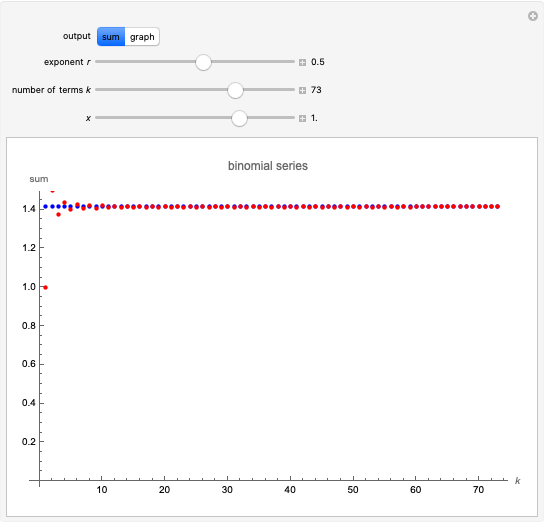
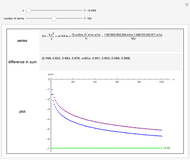
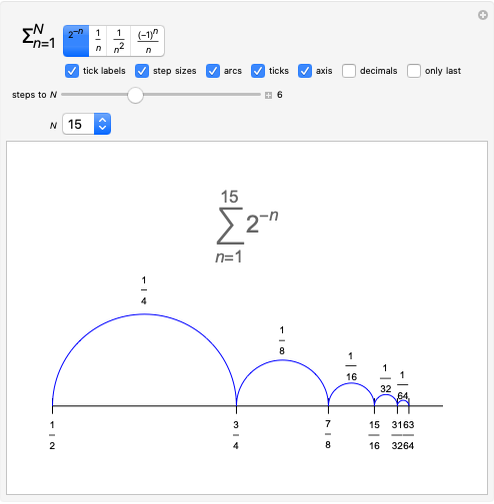
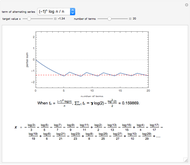
Conditionally convergent series of real numbers have the interesting property that the terms of the series can be rearranged to converge to any real value or diverge to  . In this Demonstration, you can select from five conditionally convergent series and you can adjust the target value
. In this Demonstration, you can select from five conditionally convergent series and you can adjust the target value  . The Demonstration rearranges the series, plots its
. The Demonstration rearranges the series, plots its  partial sum (the sum from 0 to the
partial sum (the sum from 0 to the  term), and shows the rearranged series.
term), and shows the rearranged series.
Contributed by: Victor Phan (October 2013)
Suggested by: Simon Tyler
Open content licensed under CC BY-NC-SA
Snapshots
Details
The five series without rearrangement are
 ,
,
 ,
,
 ,
,
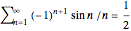 ,
,
 ,
,
where  is Euler's constant,
is Euler's constant, 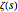 is the Riemann zeta function, and
is the Riemann zeta function, and  is the generalized Riemann zeta function.
is the generalized Riemann zeta function.
Permanent Citation