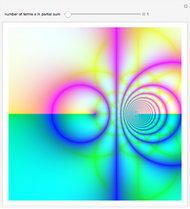
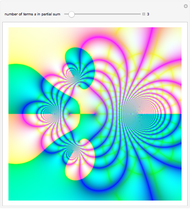
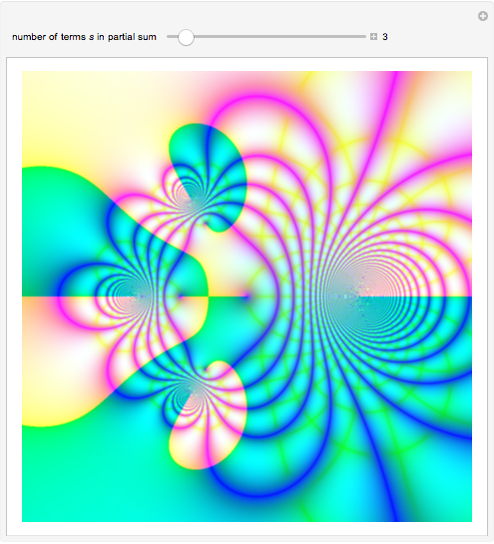
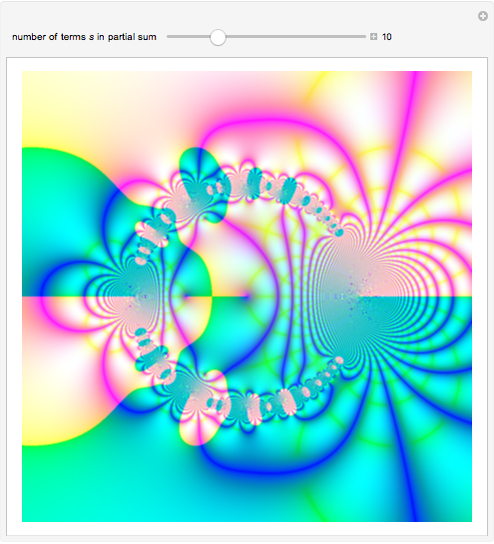
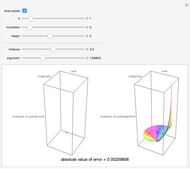
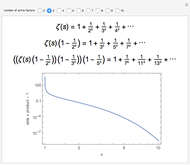
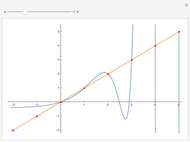
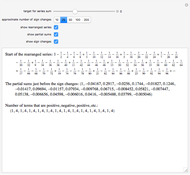
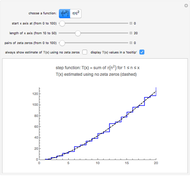
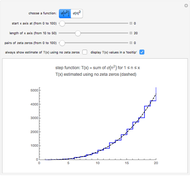
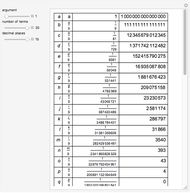
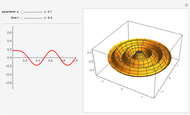
A Lambert series has the form . For bounded coefficients , the series converges in the unit disk and most poles lie on the unit circle. These series play an important role in analytic number theory and are related to the divisor function, Jacobi theta functions, the Möbius function, Euler's totient function, the Liouville function, the Ramanujan theta function, and the Riemann zeta function.