Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

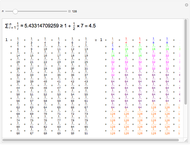
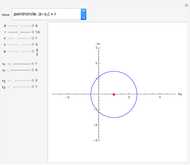
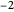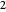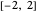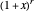Convergence of the Binomial Series

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

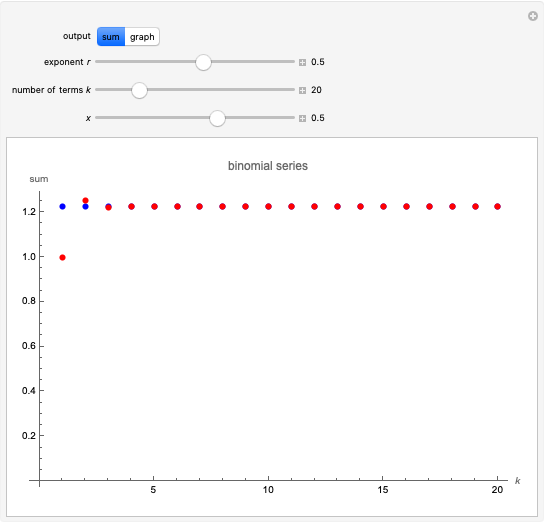
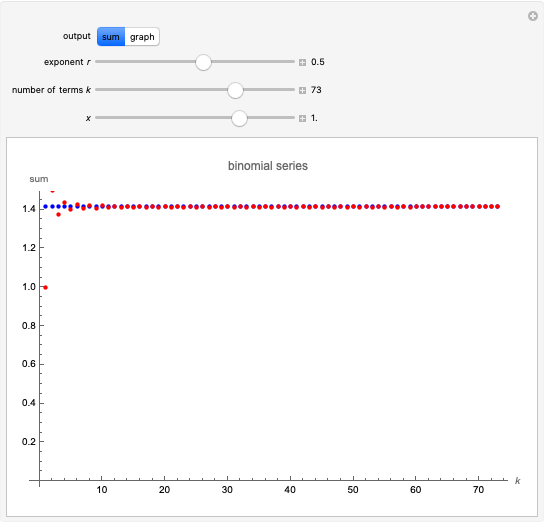
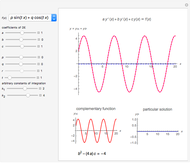
This Demonstration investigates the convergence (or otherwise) of the binomial series 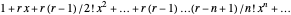, which, when convergent, converges to the function . The output (in red) is shown in two ways:

[more]

(a) the partial sum of the series, for a chosen value of between and , as you vary the number of terms ;

(b) the graph (red) of the resulting polynomial function of , as you vary , in the interval .

The function is also shown for comparison (blue).

[less]

Contributed by: Roberta Grech (November 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

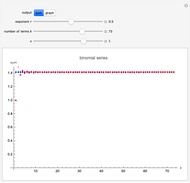
Snapshot 1: is a nonnegative integer; the series terminates

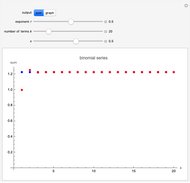
Snapshot 2: is positive but not an integer; the series converges for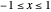

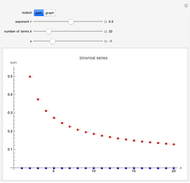
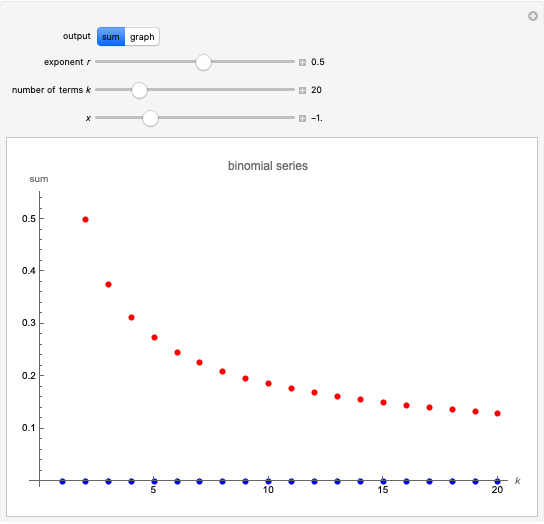
Snapshot 3: 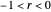; the series converges for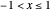

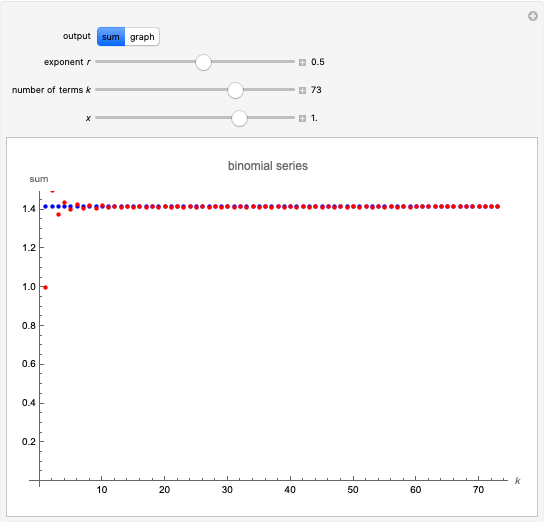
Snapshot 4: 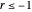; the series converges for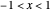

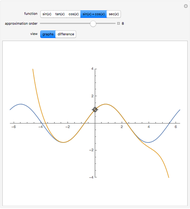
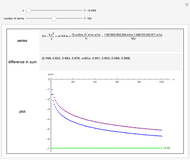
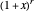Snapshot 5: the graph of the truncated binomial series (a polynomial function of ) and the function for comparison, for the same value of and the same number of terms as in Snapshot 4

Reference

[1] T. Heard, D. Martin, and B. Murphy, A2 Further Pure Mathematics, 3rd ed., London: Hodder Education, 2005 pp. 69–83.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send