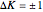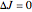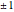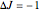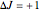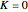Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Rovibronic Spectrum of a Perpendicular Band of a Symmetric Rotor

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

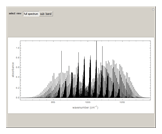
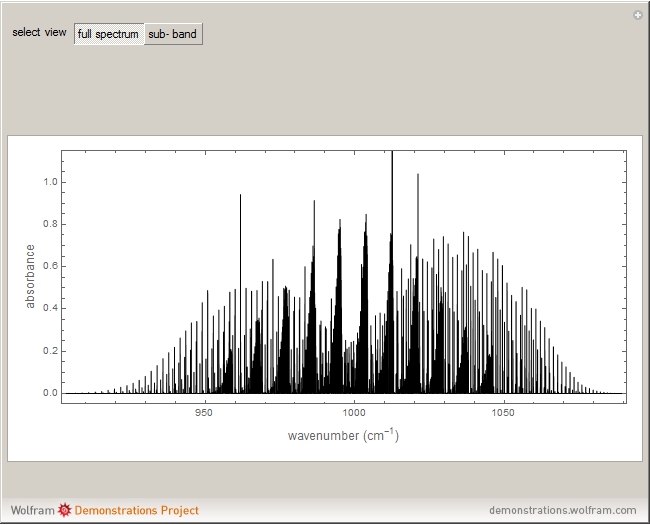
This Demonstration shows the rotationally resolved infrared spectrum of a perpendicular band of a symmetric rotor. It uses a top-down approach, with each level of options deconstructing the spectrum and revealing more details about its structure. You can view the full spectrum or choose to view the sub-bands in order to unlock the other control options and further deconstruct the sub-bands. It is also possible to zoom into any region of the spectrum by using the axis lower-limit and upper-limit boundary controls.

[more]

The vibrational energy levels for a symmetric rotor possess an inherent degeneracy because there are more than two rotation axes. This degeneracy and Coriolis splitting of the degenerate vibrational energy levels is not addressed in this Demonstration. Instead, transitions for this spectrum occur between nondegenerate vibrational energy levels. Symmetric rotors possess two axes with equal moments of inertia and a principal axis with a unique moment of inertia. When the change in the dipole moment is perpendicular to the principal axis, a perpendicular band spectrum results. For a perpendicular band, the vibrational selection rules are (where for an absorbance spectrum) and the rotational selection rules are and , for all values of , with the further restriction that . If the complete perpendicular band spectrum is deconstructed, it appears as a superposition of sub-bands, with each sub-band consisting of a branch (, , smaller wavenumbers), branch (, , middle branch), and branch (, , larger wavenumbers). Since , the series of sub-bands corresponding to are termed the "positive" sub-bands and the series of sub-bands corresponding to are termed the "negative" sub-bands. The rotational quantum number and therefore there is no negative sub-band. As a result of the restriction that , there is a decreasing number of lines observed at the beginning of each branch with increasing . The observed line intensities reflect a dependence on the rotational quantum numbers and , as well as a dependence on the thermal population of the lower state rotational energy levels. Within the positive and negative sub-bands, greater intensity is observed for the lines in which .

[less]

Contributed by: Whitney R. Hess and Lisa M. Goss (March 2011)
(Idaho State University)
Open content licensed under CC BY-NC-SA

Snapshots

Details

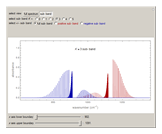
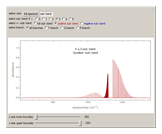
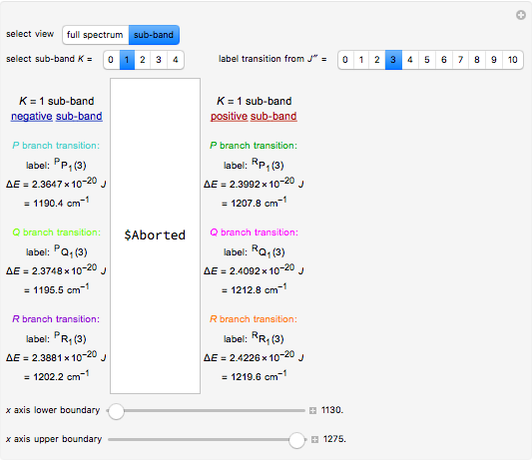
In this Demonstration, the "full spectrum" view option does not use the Manipulate functionality. Selecting "sub-band" allows you to explore the six 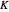sub-bands as well as to select the +/- sub-band. Selecting "positive sub-band" or "negative sub-band" shows the individual branches. Selecting " 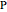branch", " branch", or " branch" allows you to view the rotational transitions (by selecting within each branch.

Lower state constants are indicated by a superscript double prime (″) and excited state constants are indicated by a superscript prime (′).

The spectrum is simulated at a temperature of 150 Kelvins and the mathematical expressions for determining line positions in the spectrum assume the centrifugal distortion constants (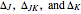) and the anharmonicity constant (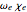) are negligible. Unequal values for the lower and excited state rotational constants 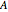and were used in order to account for the interaction of rotation and vibration (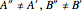). The following rotational constants were used to simulate the spectrum: , , 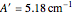, 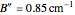and .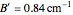

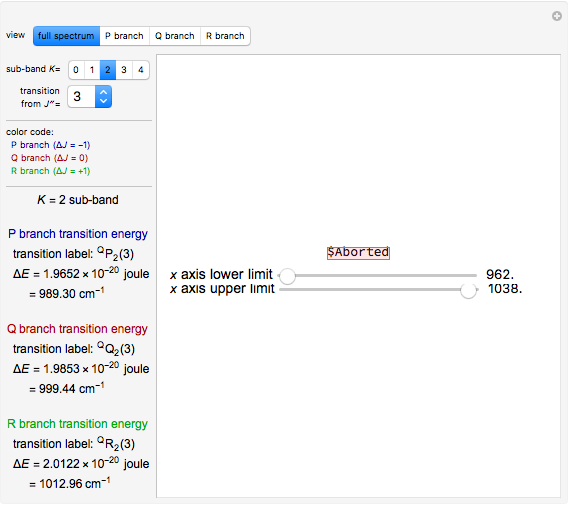
The transitions are labeled according to the format 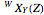, where , , , and 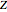are as follows:

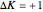: transitions with are designated with a superscript (positive sub-band) and transitions with are designated with a superscript 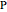(negative sub-band)

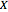: designated 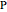, , or depending on which branch the line resides (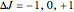, respectively)

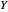: the value of 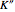is indicated by the subscript

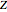: the value of 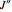is indicated within the parentheses

For example, 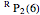indicates the line corresponding to the 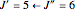transition in the 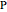branch within the positive sub-band.

Snapshots 1, 2, 3, and 4: full spectrum, full sub-band, positive sub-band, and negative sub-band views, respectively

Snapshot 5: when , , or branch is selected, the rotational transitions in each band can be explored and the spectral line corresponding to the transition of interest will be labeled according to the format previously described

References

[1] P. Atkins and J. de Paula, Physical Chemistry, New York: Oxford University Press, 2006.

[2] G. Herzberg, Molecular Spectra and Molecular Structure II. Infrared and Raman Spectra of Polyatomic Molecules, Princeton, NJ: D. Van Nostrand Company, Inc., 1945.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send