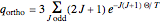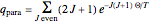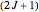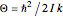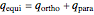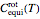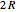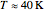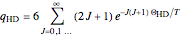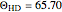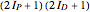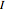Low-Temperature Heat Capacity of Hydrogen Molecules

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Hydrogen 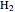 is the lowest boiling molecular species, remaining a gas down to 20K. At and above room temperature,
is the lowest boiling molecular species, remaining a gas down to 20K. At and above room temperature, 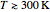 , the rotational degree of freedom is fully excited; thus the rotational contribution to heat capacity approaches its equipartition value,
, the rotational degree of freedom is fully excited; thus the rotational contribution to heat capacity approaches its equipartition value, 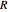 per mole. Owing to the exceptionally small moment of inertia of
per mole. Owing to the exceptionally small moment of inertia of 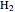 , rotation becomes inactive at temperatures below about 50K. However, the heat capacity behaves anomalously as the temperature is lowered. This anomaly was first explained by Dennison in 1927. Since
, rotation becomes inactive at temperatures below about 50K. However, the heat capacity behaves anomalously as the temperature is lowered. This anomaly was first explained by Dennison in 1927. Since 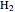 is a homonuclear molecule, only half of its rotational states are accessible. In the singlet nuclear-spin state, known as parahydrogen (p-
is a homonuclear molecule, only half of its rotational states are accessible. In the singlet nuclear-spin state, known as parahydrogen (p-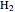 ) only even-
) only even-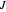 rotational states are accessible; in the triplet nuclear-spin state, known as orthohydrogen (o-
rotational states are accessible; in the triplet nuclear-spin state, known as orthohydrogen (o-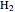 ) only odd-
) only odd-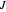 rotational states are accessible. The molecular partition functions representing the rotational and nuclear spin degrees of freedom are given by
rotational states are accessible. The molecular partition functions representing the rotational and nuclear spin degrees of freedom are given by
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
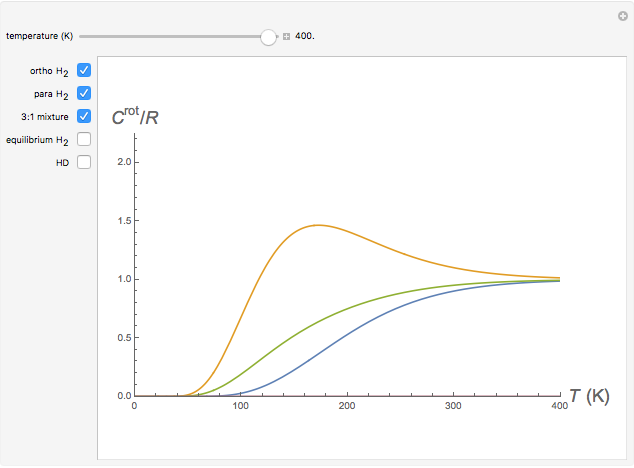
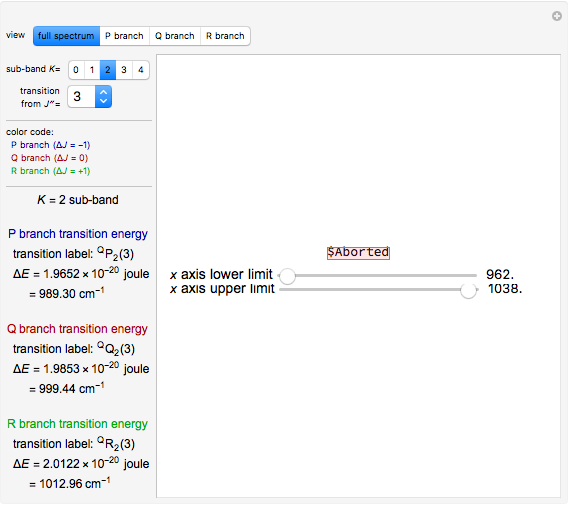
Snapshot 1: ortho and para 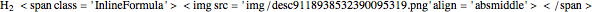 rotational heat capacities as functions of temperature
rotational heat capacities as functions of temperature
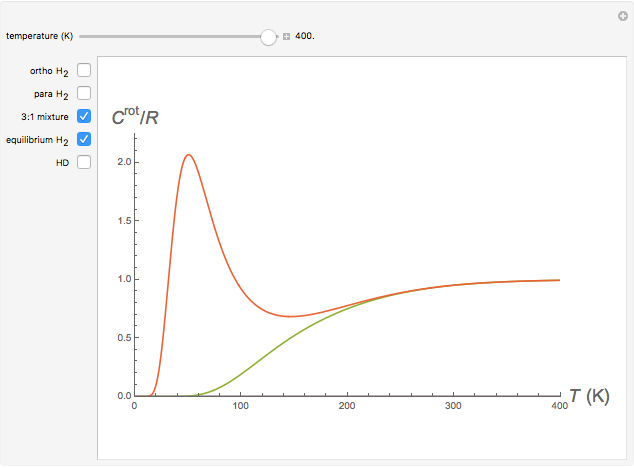
Snapshot 2: 3:1 mixture and equilibrium mixture with catalyst
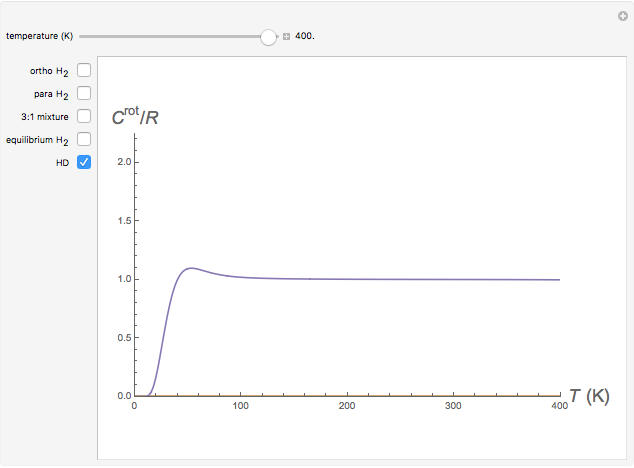
Snapshot 2: rotational heat capacity of heteronuclear HD molecule
Reference: S. M. Blinder, Advanced Physical Chemistry; A Survey of Modern Theoretical Principles, New York: Macmillan, 1969 pp. 475–478.
Permanent Citation