Schelling's Model of Residential Segregation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
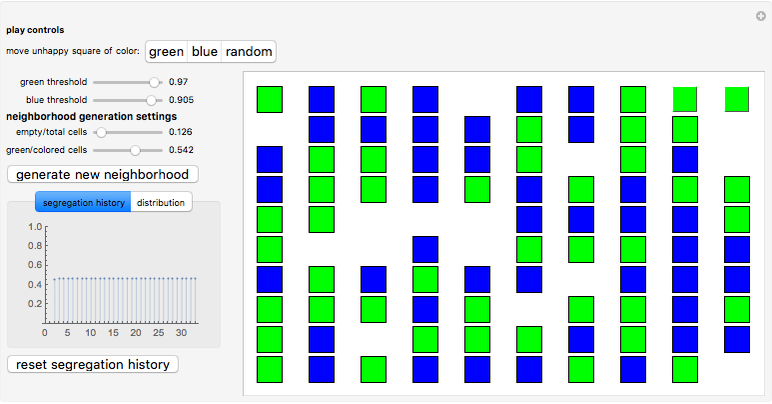
In Thomas Schelling's original model, an unhappy square, which appears as a button, chooses the closest suitable empty square when prompted to move. You can either move green squares only, blue squares only, or a random square of either color via the play controls. The threshold sliders represent the proportion of different neighbors in which squares of the corresponding colors become unhappy. For example, if the simulation is restarted with a green threshold value of 0, all the green squares will be happy unconditionally, while a green threshold value of 1 would cause all the green squares to be unhappy unconditionally. At the default value of 0.333, squares that have less than 33% of same color neighbors will be unhappy. Empty squares do not count. In this simulation, the segregation index is the average of the proportion of same-color squares for all the colored squares in the simulation.
Contributed by: Philip S. Lu (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] T. Schelling, "Dynamic Models of Segregation," Journal of Mathematical Sociology, 1, 1971 pp. 143–186.
Permanent Citation