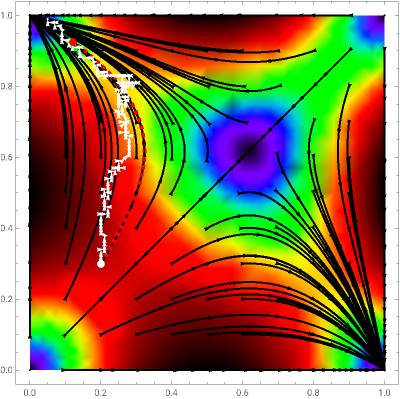
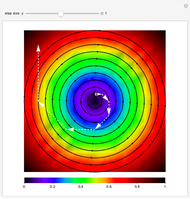
Expected Dynamics of an Intra-Population Imitation Model for Inter-Population 2x2 Symmetric Games

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
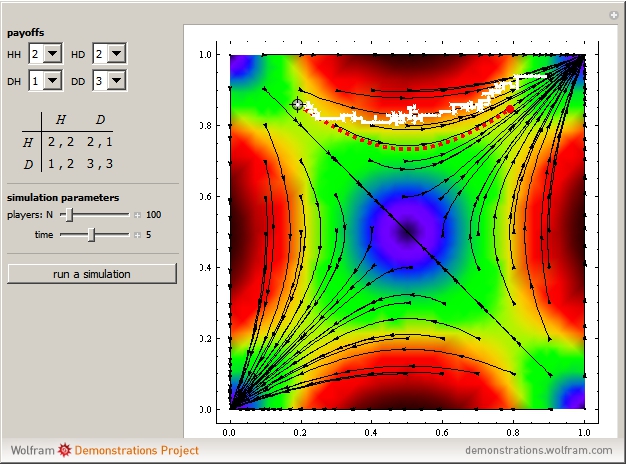
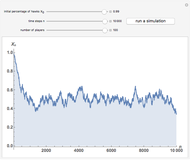
Consider two distinct populations with the same number of individuals 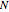 . At each iteration (of time length
. At each iteration (of time length 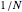 ), all individuals are randomly matched in pairs made up of one individual from each population to play a symmetric 2×2 game. The two possible actions (or pure strategies) in the game are labeled
), all individuals are randomly matched in pairs made up of one individual from each population to play a symmetric 2×2 game. The two possible actions (or pure strategies) in the game are labeled 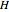 and
and  . Thus, each individual (regardless of the population to which it belongs) is either an
. Thus, each individual (regardless of the population to which it belongs) is either an 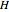 -strategist or a
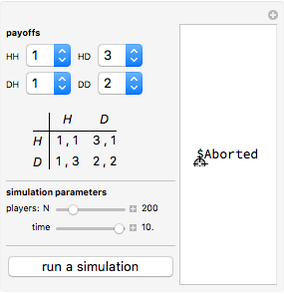
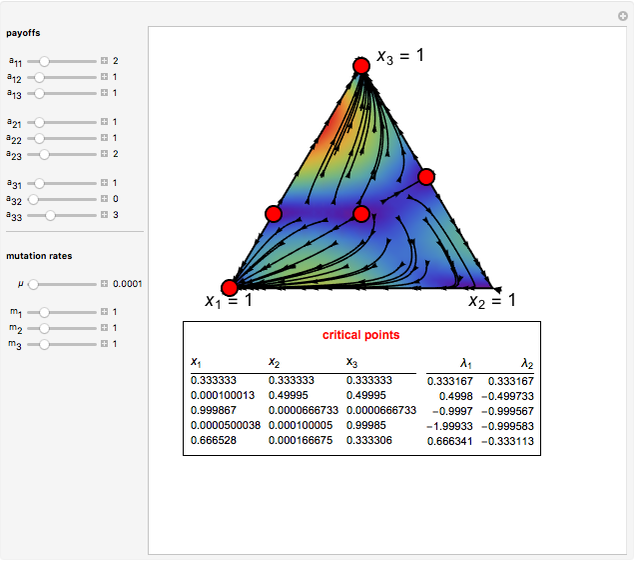
-strategist or a  -strategist. The payoffs of the game are
-strategist. The payoffs of the game are 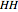 ,
,  ,
, 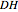 , and
, and 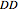 (parameters), where, for instance,
(parameters), where, for instance,  denotes the payoff obtained by an
denotes the payoff obtained by an 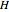 -strategist when he plays with a
-strategist when he plays with a  -strategist.
-strategist.
Contributed by: Luis R. Izquierdo and Segismundo S. Izquierdo (May 2010)
Open content licensed under CC BY-NC-SA
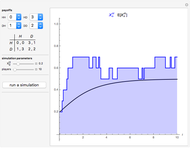
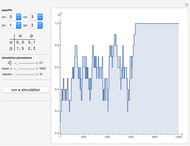
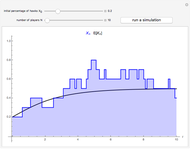
Snapshots
Details
Reference
[1] S. S. Izquierdo and L. R. Izquierdo, "Stochastic Approximation to Understand Simple Simulation Models," Journal of Statistical Physics, Dec 2012. dx.doi.org/10.1007/s10955-012-0654-z
Permanent Citation