An Intra-Population Imitation Model for Inter-Population 2x2 Symmetric Games

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
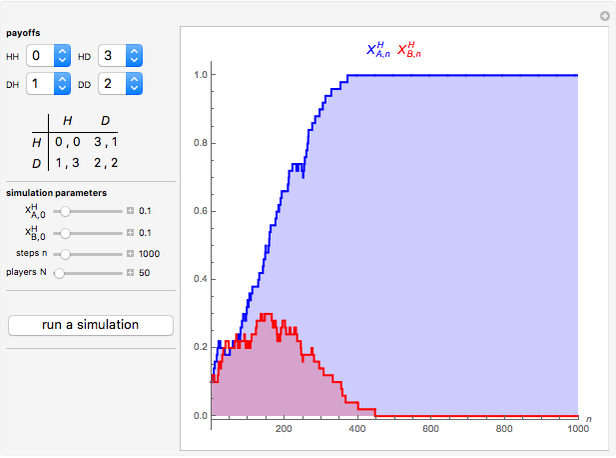
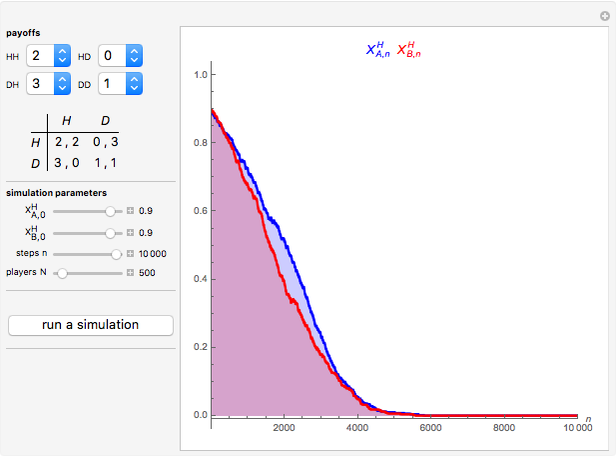
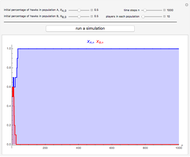
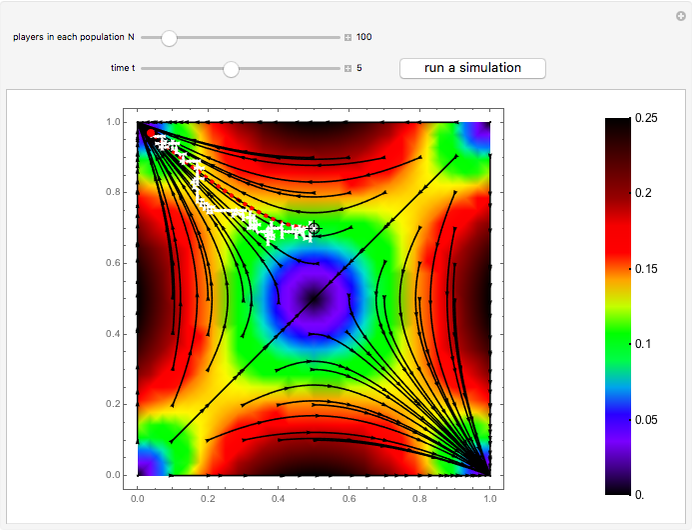
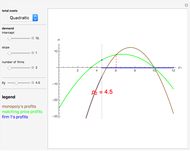
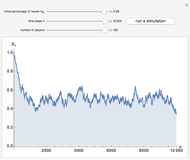
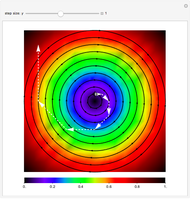
The figure shows the proportion of 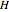 -strategists in two distinct populations (
-strategists in two distinct populations (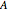 and
and 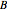 ) with the same number of individuals
) with the same number of individuals  . At each time step, all individuals are randomly matched in pairs made up of one individual from population
. At each time step, all individuals are randomly matched in pairs made up of one individual from population 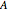 and one individual from population
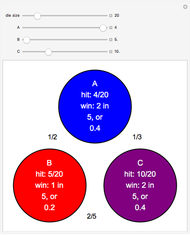
and one individual from population 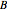 to play a symmetric 2×2 game. The two possible actions (or pure strategies) in the game are labeled
to play a symmetric 2×2 game. The two possible actions (or pure strategies) in the game are labeled 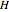 and
and  . Thus, each individual (regardless of the population to which it belongs) is either an
. Thus, each individual (regardless of the population to which it belongs) is either an 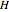 -strategist or a
-strategist or a  -strategist. The payoffs of the game are
-strategist. The payoffs of the game are 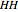 ,
, 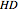 ,
, 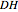 , and
, and 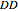 (parameters), where, for instance,
(parameters), where, for instance, 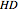 denotes the payoff obtained by an
denotes the payoff obtained by an 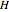 -strategist when he plays with a
-strategist when he plays with a  -strategist.
-strategist.
Contributed by: Luis R. Izquierdo and Segismundo S. Izquierdo (May 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
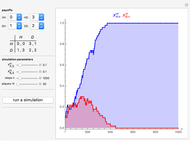
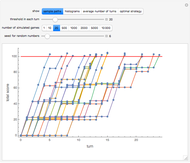
Snapshot 1: Hawk–Dove game with 50 individuals in each population (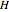 denotes the Hawk strategy and
denotes the Hawk strategy and  denotes the Dove strategy)
denotes the Dove strategy)
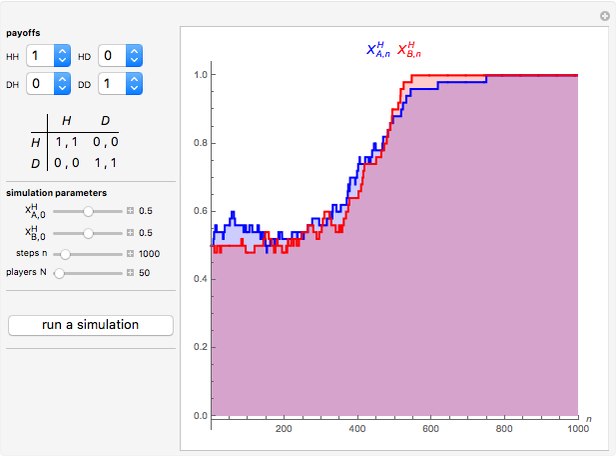
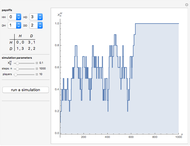
Snapshot 2: Coordination game with 50 individuals in each population (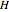 denotes "driving on my left" and D denotes "driving on my right")
denotes "driving on my left" and D denotes "driving on my right")
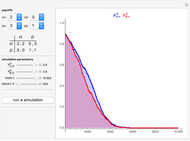
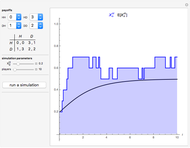
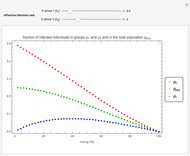
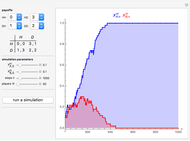
Snapshot 3: Prisoner's Dilemma game with 500 individuals in each population (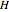 denotes the cooperative strategy and
denotes the cooperative strategy and  denotes the defective strategy)
denotes the defective strategy)
Reference
[1] S. S. Izquierdo and L. R. Izquierdo, "Stochastic Approximation to Understand Simple Simulation Models," Journal of Statistical Physics, Dec 2012. dx.doi.org/10.1007/s10955-012-0654-z
Permanent Citation