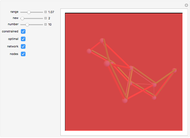
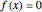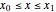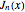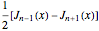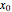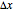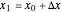A Graphically Enhanced Method for Computing Real Roots of Nonlinear Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
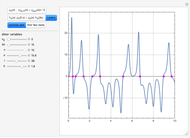
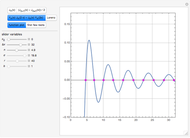
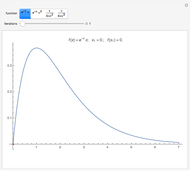
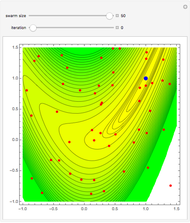
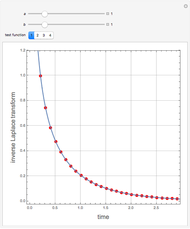
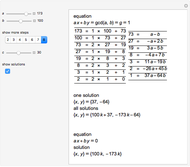
Mathematica's built-in function FindRoot is the preferred method for finding a zero of a nonlinear function 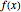 . However, determining all the zeros of
. However, determining all the zeros of 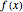 in a specified interval using FindRoot can be challenging, as this requires having good initial guesses for all the roots. In some cases, the initial guesses can be found by examining the asymptotic structure of
in a specified interval using FindRoot can be challenging, as this requires having good initial guesses for all the roots. In some cases, the initial guesses can be found by examining the asymptotic structure of 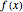 as
as  , but this is not always possible.
, but this is not always possible.
Contributed by: Housam Binous and Brian G. Higgins (February 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Lorenz equations in chaotic dynamics are
 ,
,
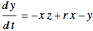 ,
,
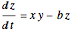 ,
,
 .
.
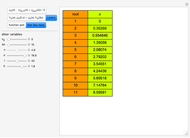
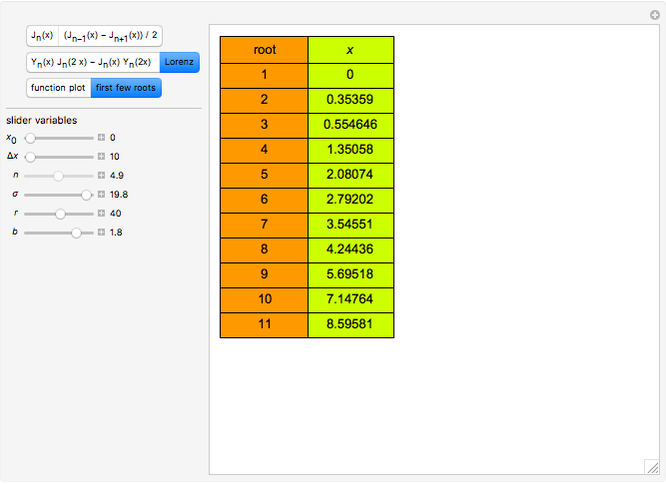
The zeros 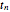 of the function
of the function  satisfy
satisfy 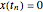 .
.
Reference
[1] S. Wagon, Mathematica® in Action: Problem Solving through Visualization and Computation, 3rd ed., Berlin: Springer-Verlag, 2010.
Permanent Citation