Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

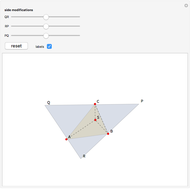
Six Triangle Orbits

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

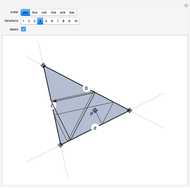
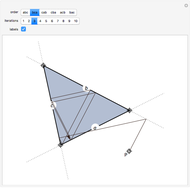
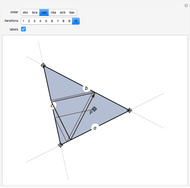
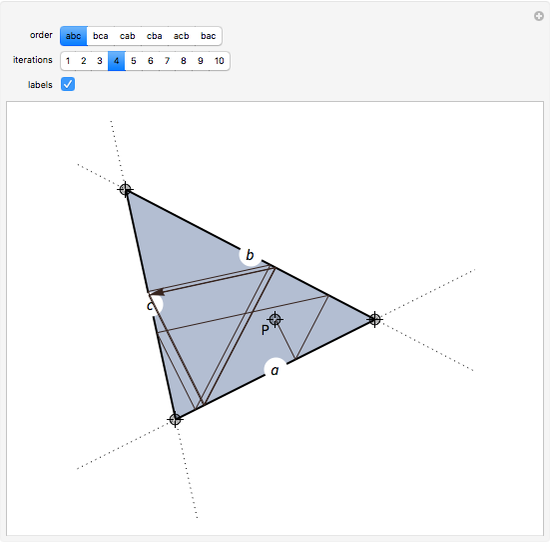
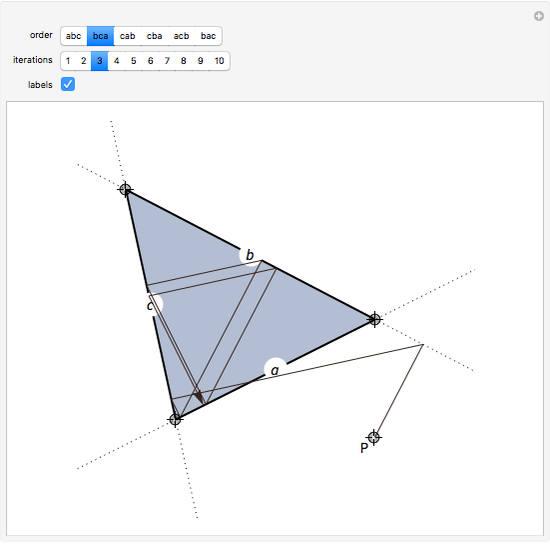
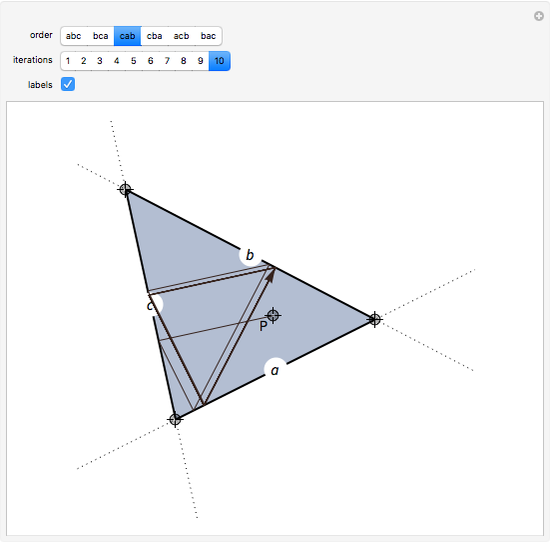
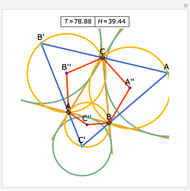
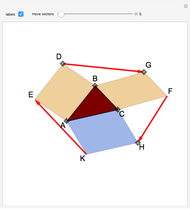
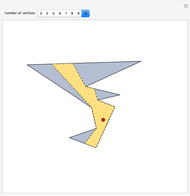
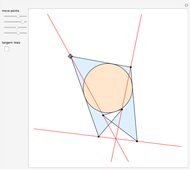
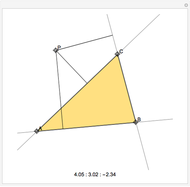
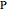Consider a triangle with sides labeled , , and a point and its trajectory as it visits each side of the triangle in some prespecified order, always taking the shortest route (by side we mean the infinite line resulting from extending the actual side of the triangle in both directions.)

[more]

We may iterate this process and notice that the trajectory converges to another triangle similar to the initial one.

The two limit triangles formed from using a side order and its reverse appear congruent and their six vertices are concentric.

This Demonstration lets you drag the vertices of the triangle, the position of point , and the visiting order so that you can investigate this phenomenon.

[less]

Contributed by: Jaime Rangel-Mondragon (August 2012)
Open content licensed under CC BY-NC-SA

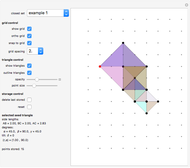
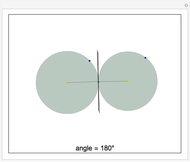
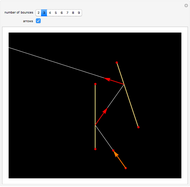
Snapshots

Details

Reference

[1] M. Carvalho and M. Hager, "Geometric Orbits," The Mathematical Intelligencer, 34(2), 2012 pp. 56–62. doi:10.1007/s00283-012-9287-y.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send