Sound Produced by Open and Closed Pipes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
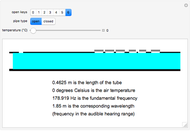
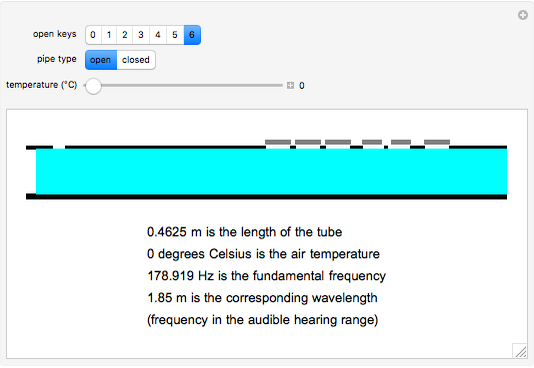
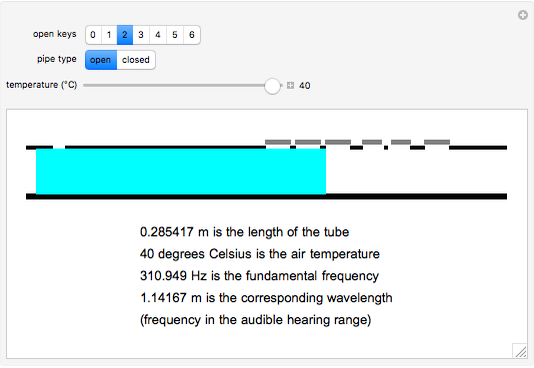
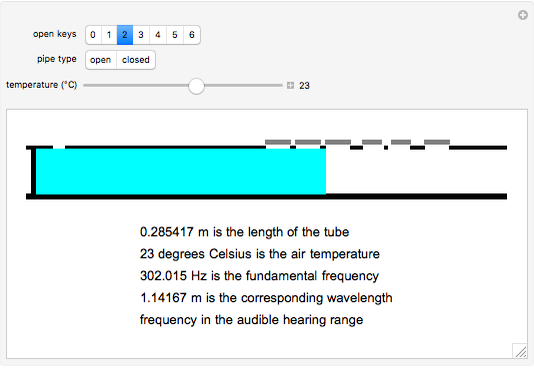
This Demonstration shows how the frequency and the corresponding wavelength in a wind instrument change depending on the unstopped length of the instrument (determined by the number of open keys), the air temperature, and whether it is an open or closed pipe. Flutes and panpipes are examples with open pipes; clarinets and saxophones are examples with closed pipes.
[more]
Contributed by: Anand Shah and Emily Steinebrey (June 2016)
Special thanks to the University of Illinois NetMath Program, and the Mathematics Department at Palatine High School.
Open content licensed under CC BY-NC-SA
Snapshots
Details
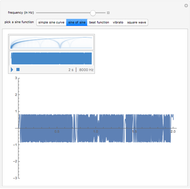
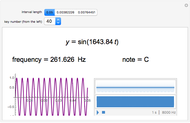
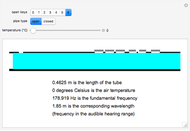
This Demonstration shows the differences in sound produced by open and closed pipes. After choosing an open or closed musical instrument, you can change the length of the air column within the pipe, which is represented by a blue rectangle, by using a slider showing the number of keys on the pipe being pressed. You can also determine the air temperature using the slider. After these are chosen, the Demonstration outputs the wavelength and frequency of the sound emitted from the pipe. Also, the audible sound that corresponds to this frequency can be played. Furthermore, it determines whether this frequency is in the audible range for humans. The purpose of our project is to show how the temperature and length of the air column within the pipe change the frequency and wavelength of the emitted pitch.
The frequency 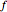 for an open pipe is given by
for an open pipe is given by 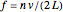 , where
, where  is the number of node-to-nodes or 1 for the fundamental frequency,
is the number of node-to-nodes or 1 for the fundamental frequency,  is the velocity of sound in air, and
is the velocity of sound in air, and 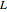 is the length of the pipe. The frequency for a closed pipe is given by
is the length of the pipe. The frequency for a closed pipe is given by  . In either case, the corresponding wavelength is
. In either case, the corresponding wavelength is 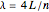 .
.
The sound velocity is given by 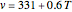 , where
, where 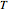 is the air temperature. The audible range for a human is between 20 and 20,000 Hz.
is the air temperature. The audible range for a human is between 20 and 20,000 Hz.
Snapshot 1: shows an open pipe with the longest pipe length and the lowest temperature
Snapshot 2: shows an open pipe with the shortest pipe length and the highest temperature
Snapshot 3: shows a closed pipe with a medium pipe length and an intermediate temperature
References
[1] A. H. Benade, Fundamentals of Musical Acoustics, New York: Oxford University Press, 1976.
[2] N. H. Fletcher and T. D. Rossing, The Physics of Musical Instruments, 2nd ed., New York: Springer, 1998.
[3] Michigan Technological University. "Flute Finger Hole Locations." (Jun 12, 2016) www.phy.mtu.edu/%7Esuits/fingers.html.
[4] T. Henderson. "The Speed of Sound." (Jun 13, 2016) www.physicsclassroom.com/class/sound/Lesson-2/The-Speed-of-Sound.
[5] R. Nave. "Resonances of Closed Air Columns." (Jun 13, 2016) hyperphysics.phy-astr.gsu.edu/hbase/waves/clocol.html.
[6] Mini Physics. "Range of Audible Frequencies." (Jun 13, 2016) www.miniphysics.com/range-of-audible-frequencies.html.
Permanent Citation