Hammer Time

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
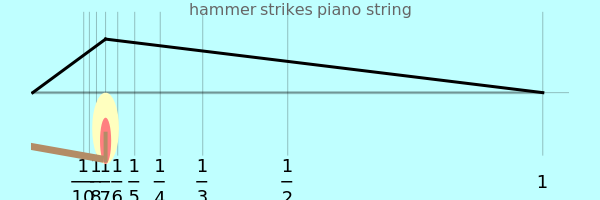
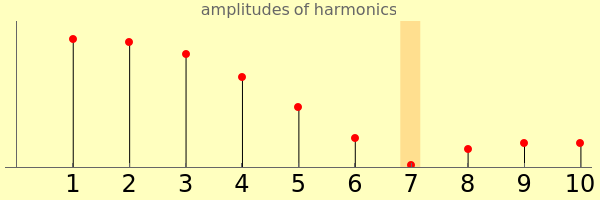
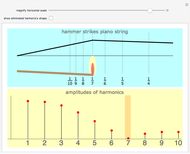
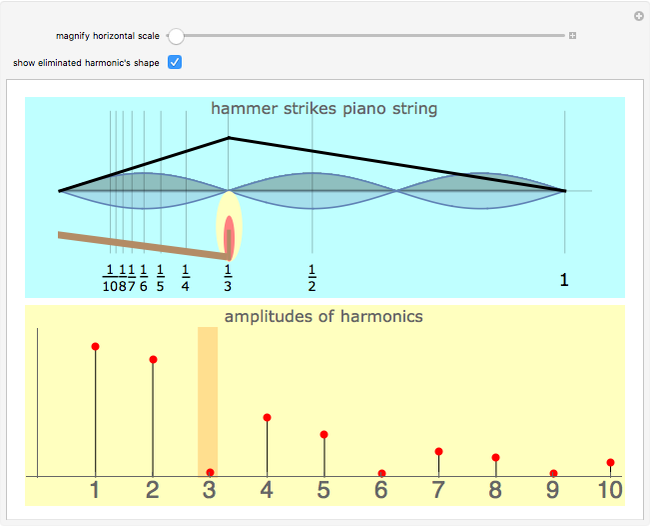
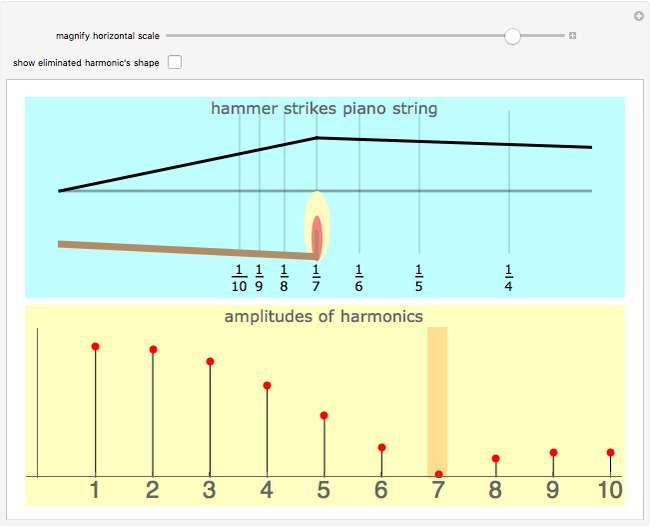
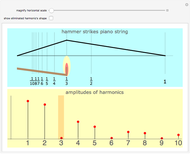
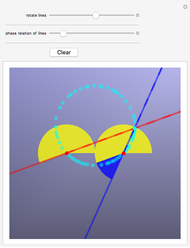
Pressing a key on a piano keyboard causes a felt-covered hammer to rise up and strike a string. In the top panel, drag the hammer back and forth along the piano string and notice the direct connection between the hammer's position—expressed as a fractional part of the string's length—and the attenuation of a specific overtone in the resulting vibrating string. Among the first eight harmonics, the seventh harmonic is the most dissonant, and so modern pianos place their hammers at one-seventh the length of the string to diminish this harmonic's contribution to the sound of the piano.
Contributed by: John Kiehl (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Snapshot 1: Dividing the string into thirds reduces the third harmonic.
Snapshot 2: By adding the plot of the third harmonic, you can see that it needs a stationary node exactly at the point where the hammer is striking the string. The hammer's action guarantees this point will be in motion, however, so the node cannot form.
Snapshot 3: You can expand the horizontal range to zoom into the higher harmonics.
Snapshot 4: If the hammer is placed very near the end of the string, all the harmonics are present in very nearly the same amount. Violinists exploit this phenomenon when they bow near the bridge of the violin—a bowing technique called "pontecello". The resulting timbre, rich in higher overtones, is very "glassy" or strident sounding.
Snapshot 5: Another bowing technique for violinists is "sul tasto", which means to play over the finger board, near the center of the string. This timbre is duller or "softer" sounding than the "ordinario" bowing technique. Guitarists also can pick their strings in these different places to create a range of timbres.
There are three major principles at work in this Demonstration. First, from Fourier theory is the notion that any continuous function can be decomposed into a series of sine waves, and so the shape of the vibrating string can be analyzed from the perspective of a sum of its harmonics. Second, the physics of the vibrating string makes a demand on the harmonics as well. For example, the mere fact that the two ends of the string are fastened to the sound board and cannot move means that the modes of vibration must be sine waves that have half-wavelengths that integrally divide the length of the string. This gives rise to the nodal points along the string for each harmonic. Third, the subjective sense of what sounds sonorous is based on the simple integer relations of the harmonics of a vibrating string: a 2:1 ratio is an octave, a 3:1 ratio is a perfect fifth, and a 5:1 is a major third.
The terms overtone and harmonic are often used interchangeably, especially when speaking in a casual, musical way. More precisely, harmonic is used to discuss modes of vibrations that are integer multiples of the object's fundamental frequency, while overtone is more generally used to refer to any vibration, integrally related or not to the fundamental. Percussion instruments like drums and bells lack a strong sense of pitch specifically because they are rich in overtones that are not integer multiples of their lowest, fundamental frequency, i.e. they have many inharmonic overtones. A second difference between an overtone and a harmonic is the conventional numbering scheme used to discuss them. The lowest vibrational mode is called the fundamental and is accompanied by higher overtones. However, since the fundamental can be referred to as the "first" harmonic, the "second" harmonic is equivalent to the "first" overtone .
In the name of full disclosure it should be noted that the triangular-shaped initial condition implied by the graphic is in fact a gross oversimplification of the physics of a hammer striking a piano string. Serious researchers divide the striking of a piano string into three parts: (1) the initial contact; (2) the continued contact (referred to as "bow and arrow" since the hammer is now analogous to an arrow being shot from a drawn bow); and (3) the freely moving string. Each moment has a radically different physics and geometry. For example, see A. H. Benade's 1983 paper: http://ccrma.stanford.edu/marl/Benade/documents/Benade-StruckPiano-1983.pdf.
Permanent Citation
"Hammer Time"
http://demonstrations.wolfram.com/HammerTime/
Wolfram Demonstrations Project
Published: March 7 2011