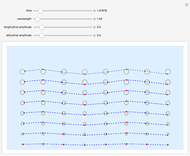
Resonance in Open and Closed Pipes

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
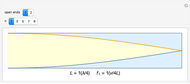
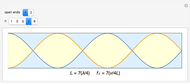
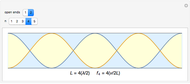
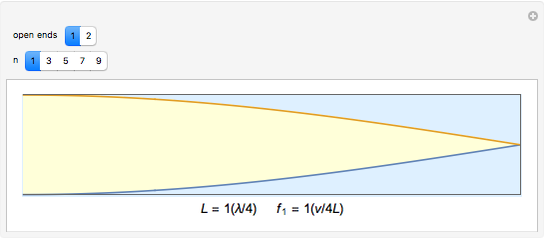
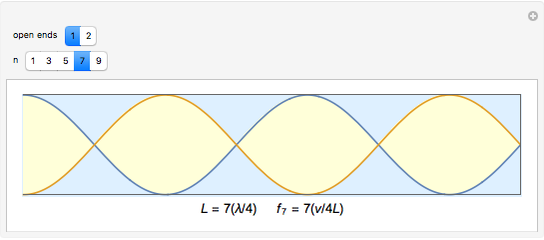
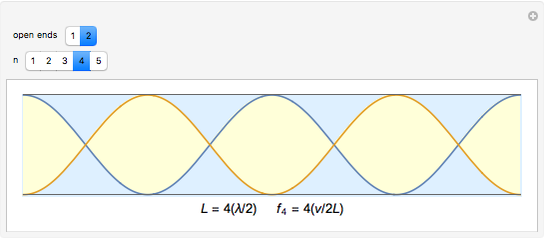
A system exhibiting resonance oscillates with a large amplitude. This occurs at the frequency of a fundamental mode or a multiple thereof, which is one of its harmonics (or overtones). The graphic shows a pipe containing air with either closed or open ends. Sine waves represent standing waves with specified wavelengths and frequencies. Nodes are points of zero amplitude while antinodes are points of maximum amplitude. A closed end is a node and an open end is an antinode, which is essential in explaining how wind instruments work.
Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The wavelengths  and frequencies
and frequencies 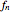 for resonance in air columns for a pipe of length
for resonance in air columns for a pipe of length 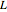 moving at the speed of sound
moving at the speed of sound  are: with one open end,
are: with one open end, 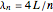 and
and  , for
, for  odd; and with two open ends,
odd; and with two open ends,  and
and 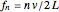 , for
, for  even.
even.
See the Wikipedia entry for Resonance.
Permanent Citation
"Resonance in Open and Closed Pipes"
http://demonstrations.wolfram.com/ResonanceInOpenAndClosedPipes/
Wolfram Demonstrations Project
Published: March 7 2011