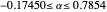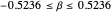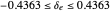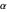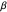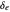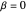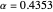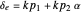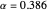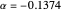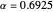Static Longitudinal Stability of Fixed Wing Aircraft

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
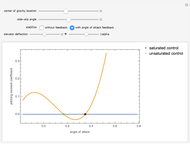
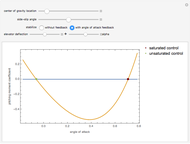
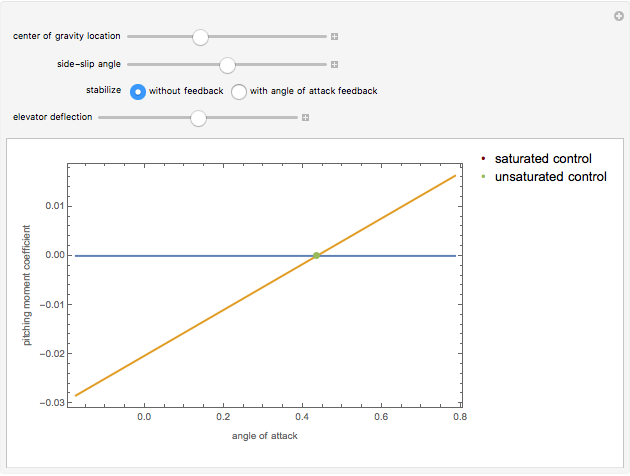
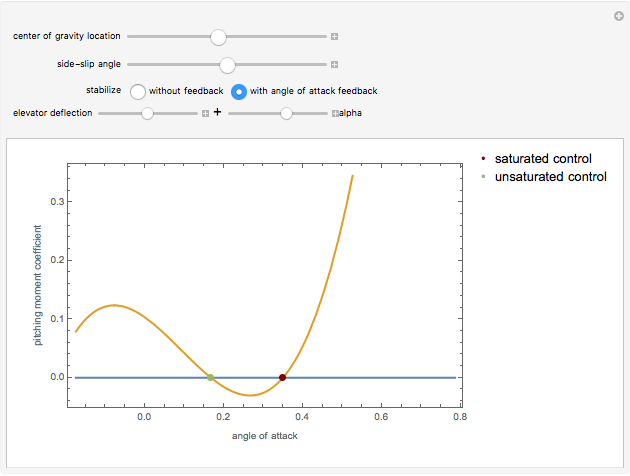
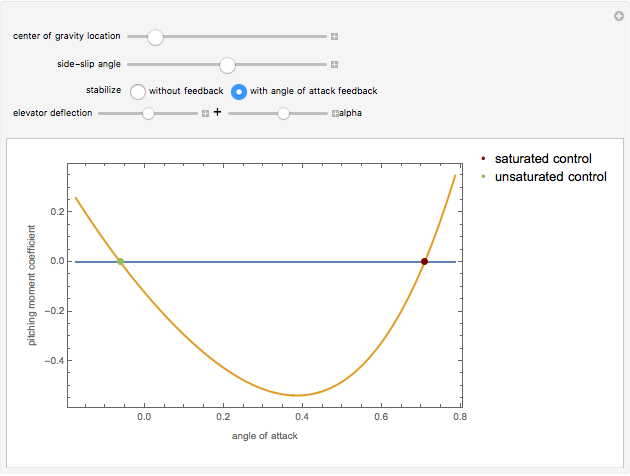
For an aircraft to achieve static longitudinal stability, its pitching moment must be perfectly balanced. The pitching moment coefficient, 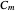 , for a fixed-wing aircraft depends on several factors, notably, the angle of attack, center of gravity location, and the elevator deflection. In addition to being balanced, stability is an important consideration. For stability, the pitch stiffness of the aircraft given by the stability derivative
, for a fixed-wing aircraft depends on several factors, notably, the angle of attack, center of gravity location, and the elevator deflection. In addition to being balanced, stability is an important consideration. For stability, the pitch stiffness of the aircraft given by the stability derivative 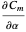 (where
(where  is the angle of attack) must be negative. This ensures a restoring moment if the aircraft is disturbed from its equilibrium position due to disturbances like wind gusts. Discussions on static longitudinal stability can be found in several texts (for example, Etkin and Reid 1996).
is the angle of attack) must be negative. This ensures a restoring moment if the aircraft is disturbed from its equilibrium position due to disturbances like wind gusts. Discussions on static longitudinal stability can be found in several texts (for example, Etkin and Reid 1996).
Contributed by: Suba Thomas (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References:
B. Etkin and L. D. Reid, Dynamics of Flight: Stability and Control, 3rd ed., New York: John Wiley & Sons, 1996.
E. A. Morelli, "Global Nonlinear Parametric Modeling with Application to F-16 Aerodynamics," in Proceedings of the American Control Conference, Philadelphia, 1998 pp. 997–1001.
Permanent Citation