Stokes Boundary Layer

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
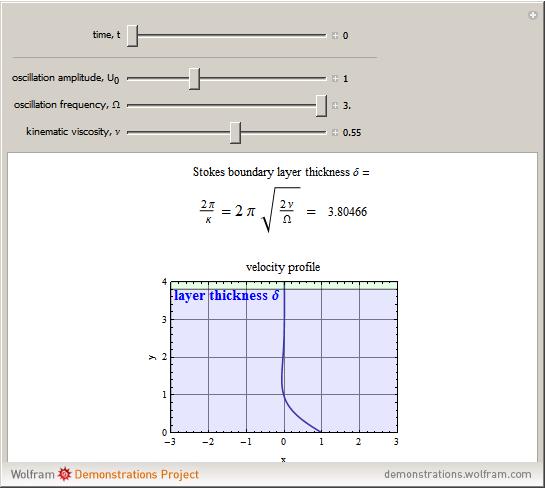
The Stokes boundary layer (also called the oscillatory boundary layer) is a special case of the Navier–Stokes equations of fluid dynamics in which an analytical solution can be found. It occurs when a viscous fluid flows over a smooth plate that oscillates parallel to the flow, which needs to be laminar (low Reynolds number).
[more]
Contributed by: Jorge García Tíscar (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
As explained in the caption, this specific situation of laminar flow of a viscous fluid near a plate that oscillates with velocity 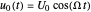 provides one of the few pure analytical solutions of the Navier–Stokes equations:
provides one of the few pure analytical solutions of the Navier–Stokes equations:
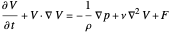 ,
,
where 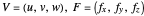 . If we assume the flow to be unidimensional, with the only nonzero component of the velocity being
. If we assume the flow to be unidimensional, with the only nonzero component of the velocity being  , parallel to the plate, only one component of the three-dimensional Navier–Stokes equation remains:
, parallel to the plate, only one component of the three-dimensional Navier–Stokes equation remains:
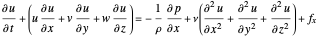 .
.
Since we assume that the flow is incompressible and that other forces are not present, the above equation reduces to
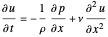 .
.
Now, as the pressure gradient 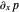 does not change with
does not change with  but only with time, its value must be the same for all
but only with time, its value must be the same for all  . Since as
. Since as  goes to infinity, the velocity of the fluid,
goes to infinity, the velocity of the fluid,  , goes to zero, the pressure gradient there must be zero; therefore it must be zero for all
, goes to zero, the pressure gradient there must be zero; therefore it must be zero for all  , and we can write
, and we can write
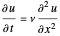 .
.
We can solve this second-order partial differential equation, assuming a solution for 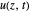 of the form
of the form 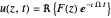 , so the equation can be written as
, so the equation can be written as
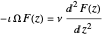 .
.
With the boundary conditions of no slip at the plate, 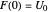 , and zero velocity far away from it,
, and zero velocity far away from it, 
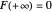 , we can obtain the analytical solution of the velocity profile:
, we can obtain the analytical solution of the velocity profile:
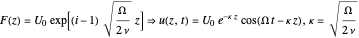 .
.
The parameter  can be seen as a kind of "wavenumber", associated with a dimension or "wavelength":
can be seen as a kind of "wavenumber", associated with a dimension or "wavelength":
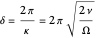 .
.
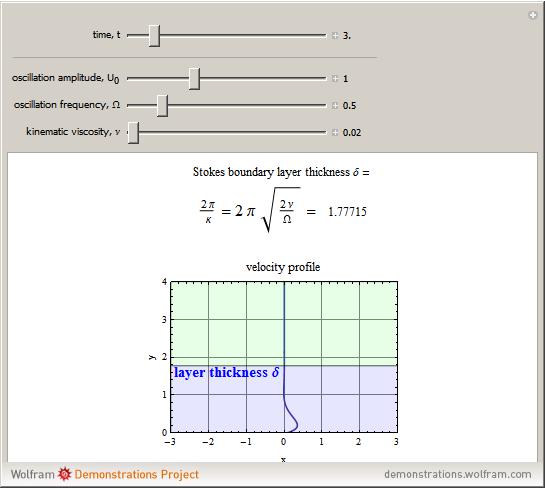
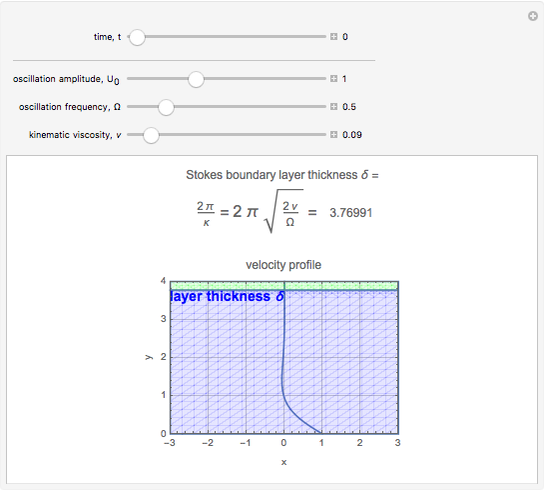
This is known as the Stokes boundary layer thickness. From the velocity equation, we can see that the oscillation of the plate propagates as a damped wave along the  direction, and that the amplitude of this wave reduces to
direction, and that the amplitude of this wave reduces to 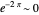 at a distance
at a distance  from the plate.
from the plate.
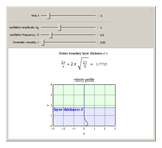
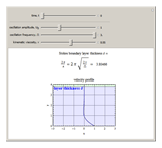
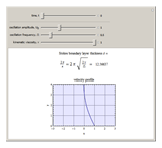
This Demonstration shows how the thickness  changes with the viscosity of the fluid, the oscillation frequency of the plate, and the evolution in time of the velocity profile
changes with the viscosity of the fluid, the oscillation frequency of the plate, and the evolution in time of the velocity profile 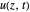 . Set the "time" slider motion to automatic and change the conditions of the problem to see how each one affects the velocity profile, which can be easily seen after a few moments.
. Set the "time" slider motion to automatic and change the conditions of the problem to see how each one affects the velocity profile, which can be easily seen after a few moments.
Snapshot 1: viscosity greatly affects the layer thickness
Snapshot 2: frequency also affects the layer thickness
Snapshot 3: oscillation amplitude is best shown at 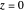
Permanent Citation