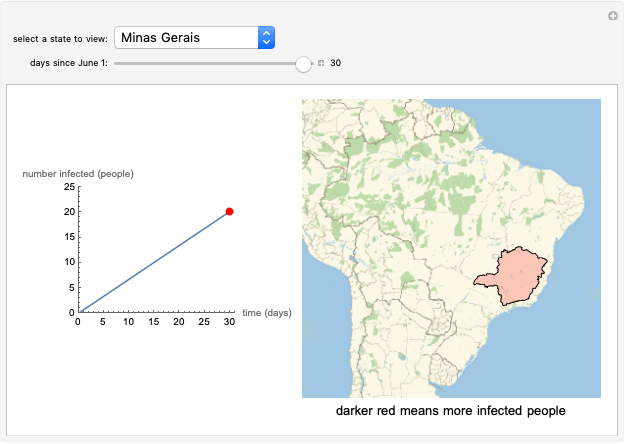
Survival Rate for Patients with Pulmonary Arterial Hypertension (PAH)

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
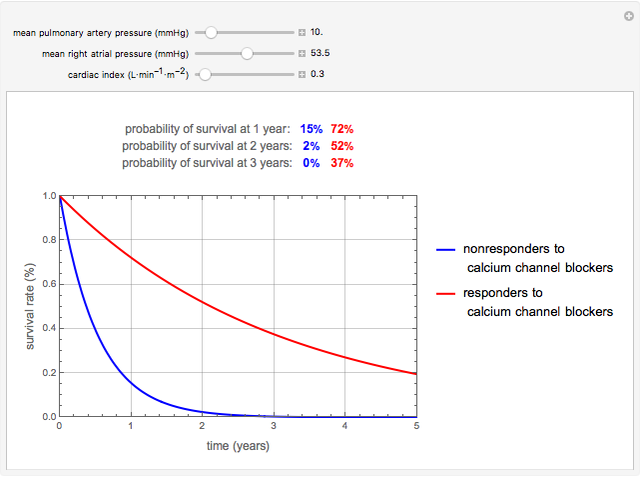
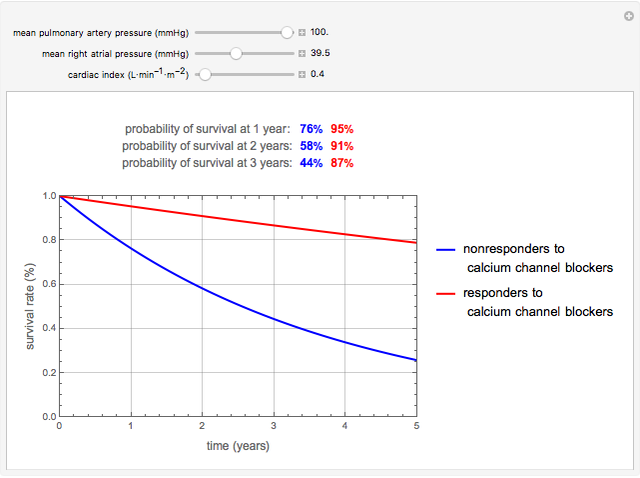
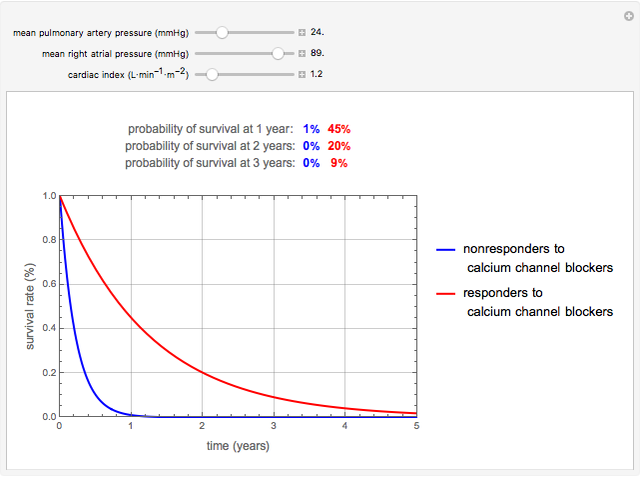
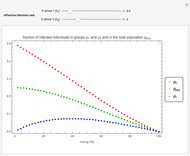
This Demonstration determines the survival rate over time for patients with pulmonary arterial hypertension (PAH) for nonresponders to calcium channel blockers and responders to calcium channel blockers based on the patient's mean pulmonary artery pressure, mean right atrial pressure, and cardiac index. PAH is a progressive disease characterized by the initial blockage and later destruction of the pulmonary arteries that directly causes right ventricular failure and death. The multivariate survival equations used in this Demonstration predict a patient's chance of survival over a period of time and are based on exponential regression analysis. The pulmonary hypertension connection (PHC) equations or the survival equations are 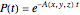 , where
, where 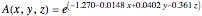 for nonresponders to calcium channel blockers and
for nonresponders to calcium channel blockers and 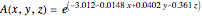 for responders to calcium channel blockers. In these equations,
for responders to calcium channel blockers. In these equations,  is the probability of patient survival,
is the probability of patient survival,  is the time in years,
is the time in years,  is the mean pulmonary artery pressure (mmHg),
is the mean pulmonary artery pressure (mmHg),  is the mean right atrial pressure (mmHg), and
is the mean right atrial pressure (mmHg), and  is the cardiac index (
is the cardiac index (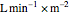 ).
).
Contributed by: Pooja Chandrashekar (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Using sliders, you can vary the mean pulmonary artery pressure, mean right atrial pressure, and cardiac index. For healthy patients, the mean pulmonary artery pressure is approximately 15 mmHg, the mean right atrial pressure is lower than 5 mmHg, and the cardiac index is in the range 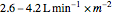 . In order to account for the inclusion of patients who responded to treatment with calcium channel blockers, two separate functions of the form
. In order to account for the inclusion of patients who responded to treatment with calcium channel blockers, two separate functions of the form 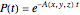 were developed to predict an individual patient’s chances of survival for responders (positive response to an acute vasodilatory challenge) and nonresponders (negative response to an acute vasodilatory challenge) using exponential regression analysis. The survival rate is the probability of survival at a certain point in time and for each combination of parameters. The probability of survival is also displayed as a percentage for one year, two years, and three years for both nonresponders and responders. In each case, we can see that the probability of survival at one, two, and three years is significantly higher for responders as compared to nonresponders. These functions were derived and developed in [1] as an improvement over the traditional NIH risk stratification equation to predict survival probability for PAH patients. While the NIH function underestimated survival in several groups of patients, this new set of functions provides a much better approximation of survival and performed well when tested against data obtained from survival studies of PAH. These functions are used to understand the effect of calcium channel blockers on PAH patients and to determine prognosis.
were developed to predict an individual patient’s chances of survival for responders (positive response to an acute vasodilatory challenge) and nonresponders (negative response to an acute vasodilatory challenge) using exponential regression analysis. The survival rate is the probability of survival at a certain point in time and for each combination of parameters. The probability of survival is also displayed as a percentage for one year, two years, and three years for both nonresponders and responders. In each case, we can see that the probability of survival at one, two, and three years is significantly higher for responders as compared to nonresponders. These functions were derived and developed in [1] as an improvement over the traditional NIH risk stratification equation to predict survival probability for PAH patients. While the NIH function underestimated survival in several groups of patients, this new set of functions provides a much better approximation of survival and performed well when tested against data obtained from survival studies of PAH. These functions are used to understand the effect of calcium channel blockers on PAH patients and to determine prognosis.
Reference
[1] T. Thenappan, S. J. Shah, S. Rich, L. Tian, S. L. Archer, and M. Gomberg-Maitland, "Survival in Pulmonary Arterial Hypertension: A Reappraisal of the NIH Risk Stratification Equation," European Respiratory Journal, 35(5), 2010 pp. 1079–1087.
Permanent Citation