Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Tangents to the Circumcircle at the Vertices

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

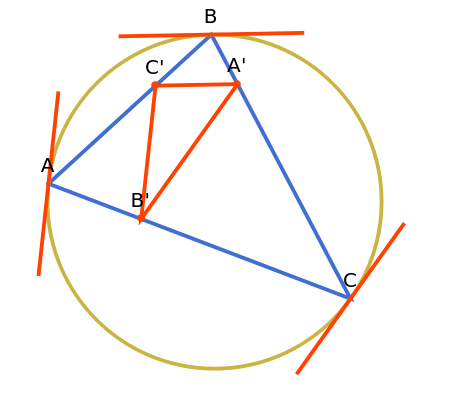
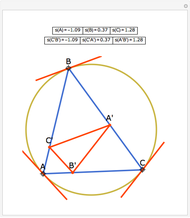
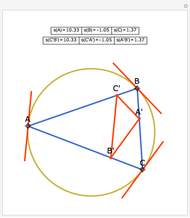
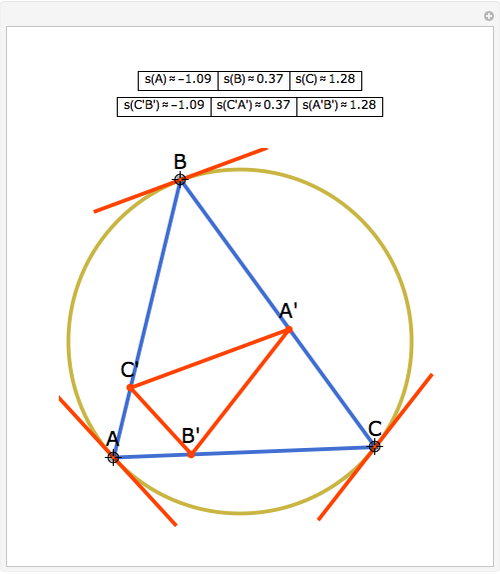
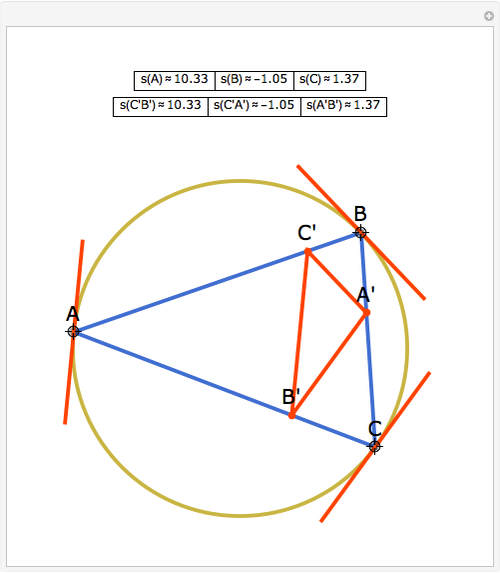
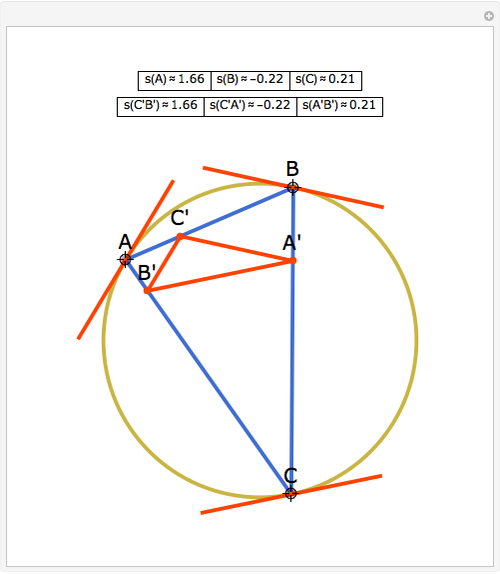
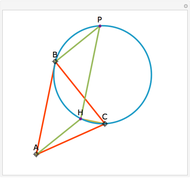
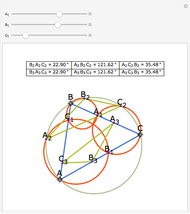
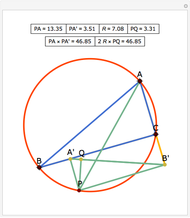
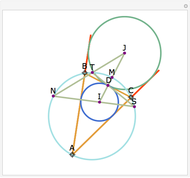
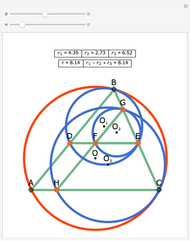
Let ABC be a triangle and A'B'C' its orthic triangle. The tangent lines to the circumcircle of ABC at the vertices are parallel to the corresponding sides of the orthic triangle A'B'C'. For example, the tangent line at A is parallel to B'C'.

[more]

In the table, is the slope of the tangent line to the circumcircle at the point X and is the slope of the line segment XY.

[less]

Contributed by: Jay Warendorff (March 2011)
Open content licensed under CC BY-NC-SA

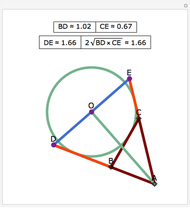
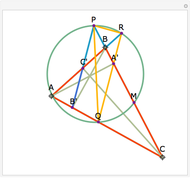
Snapshots

Details

The orthic triangle is formed by the feet of the altitudes of a triangle.

See Exercise 270(c) in R. A. Johnson, Advanced Euclidean Geometry, Mineola, NY: Dover, 2007 p. 172.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send