The Hazard of Multiple Comparisons

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
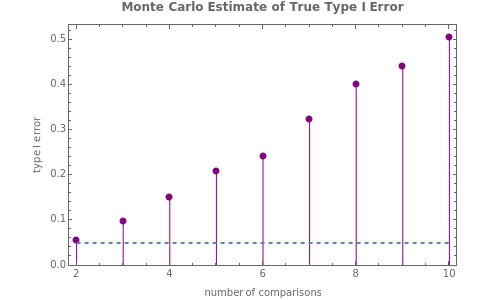
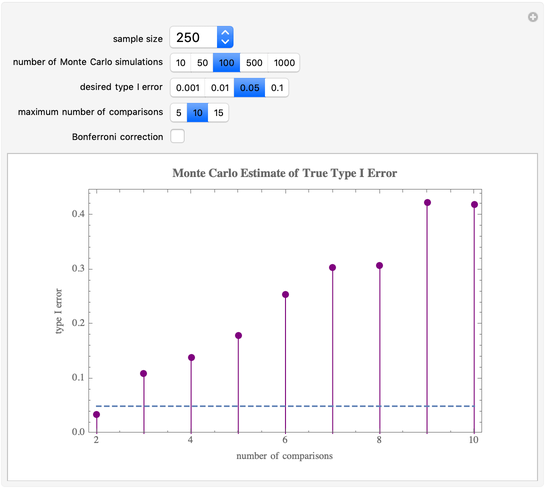
The need to compare means of multiple datasets arises frequently in data analysis. Procedures such as ANOVA detect a difference among means but do not determine which of them are significantly different. We may be tempted to simply run  -tests on each pair of means to detect these differences, but, as this Demonstration shows, doing so leads to a dramatic inflation of the true type I error (rate of false positives). Thus, when multiple comparisons are needed, a correction for this error inflation must be used.
-tests on each pair of means to detect these differences, but, as this Demonstration shows, doing so leads to a dramatic inflation of the true type I error (rate of false positives). Thus, when multiple comparisons are needed, a correction for this error inflation must be used.
Contributed by: Andy Ross (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
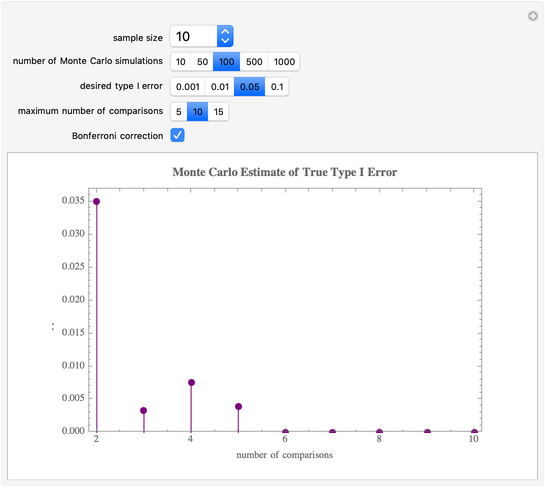
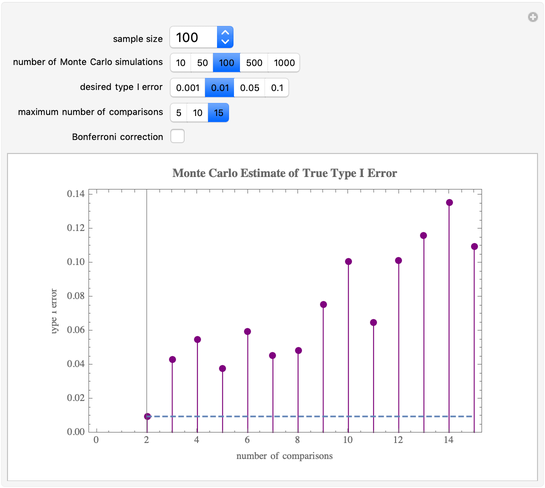
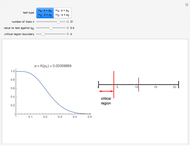
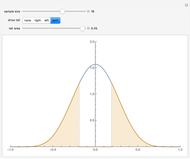
All datasets are simulated from a normal (0, 1) distribution and every pairwise comparison is made. The dashed line represents the desired type I error threshold and the individual points are the type I error rates observed in the simulation. The Bonferroni correction used here simply sets the type I threshold  in the Monte Carlo simulation to
in the Monte Carlo simulation to  where
where  is the number of pairwise comparisons being made. Details about the Bonferroni method and other correction methods can be found at Bonferroni's method.
is the number of pairwise comparisons being made. Details about the Bonferroni method and other correction methods can be found at Bonferroni's method.
Permanent Citation