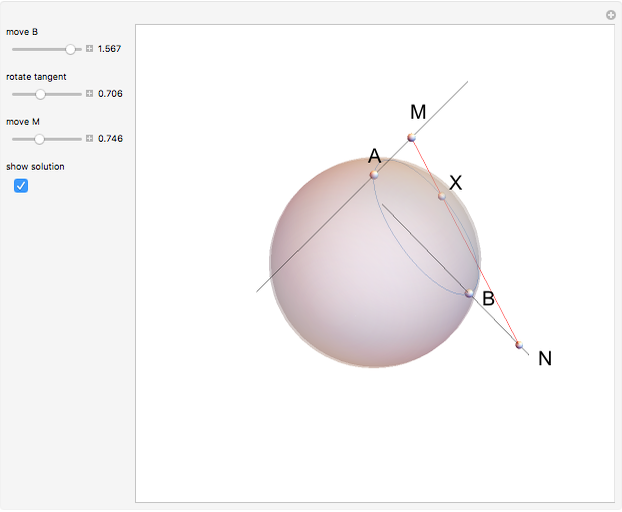
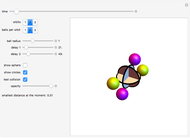
Three Tangents to a Sphere

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
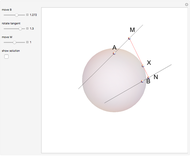
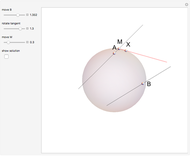
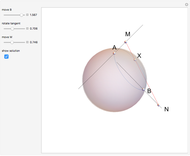
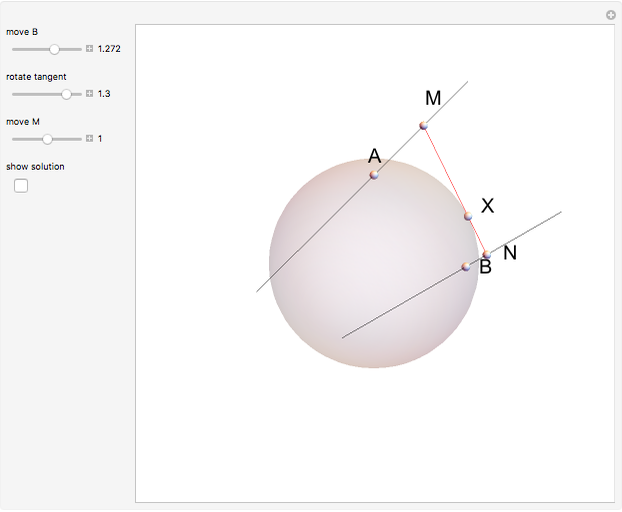
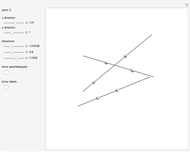
Two lines,  and
and  , are tangent to a sphere at points
, are tangent to a sphere at points  and
and  , respectively. Find the line
, respectively. Find the line  that is tangent to the sphere and intersects the other two tangents.
that is tangent to the sphere and intersects the other two tangents.
Contributed by: Izidor Hafner (April 2017)
Open content licensed under CC BY-NC-SA
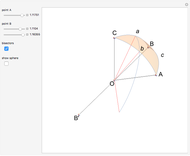
Snapshots
Details
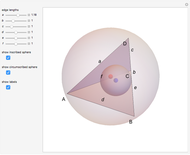
If  and
and  are unit vectors parallel to
are unit vectors parallel to  and
and  , a point
, a point  lies on a plane that contains the line
lies on a plane that contains the line  and forms equal angles with
and forms equal angles with  and
and  . There are two such planes; one is parallel to
. There are two such planes; one is parallel to  , the other to
, the other to  . So all
. So all  are in the intersections of these two planes with the sphere, that is, on two circles on the sphere. In this Demonstration we show one of them [1, p. 224].
are in the intersections of these two planes with the sphere, that is, on two circles on the sphere. In this Demonstration we show one of them [1, p. 224].
Reference
[1] V. V. Prasolov and I. F. Sharygin, Problems in Stereometry (in Russian), Moscow: Nauka, 1989.
Permanent Citation