Tiling the Hyperbolic Plane with Regular Polygons
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
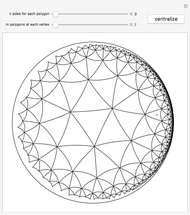
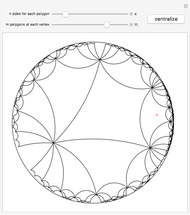
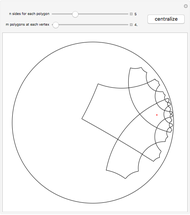
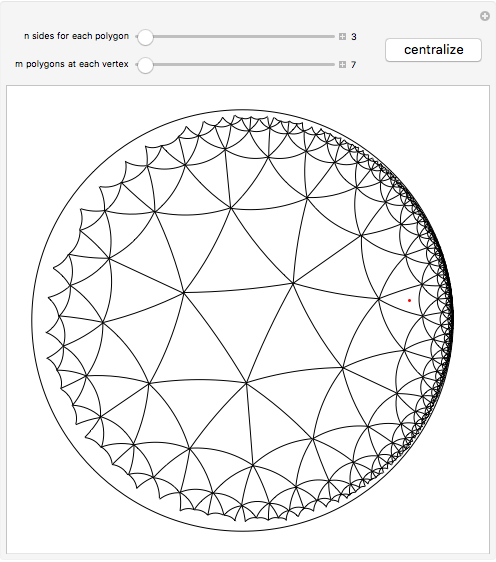
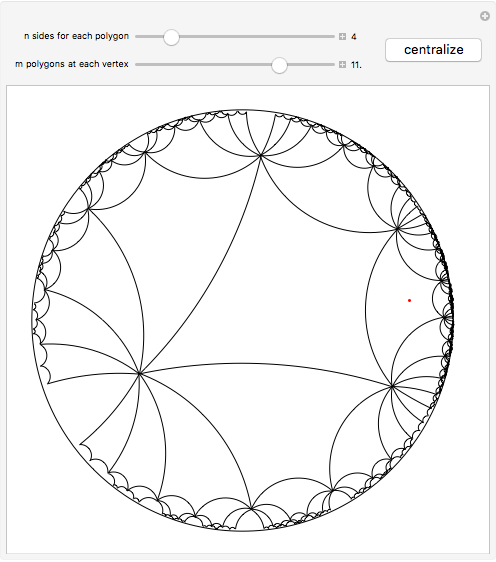
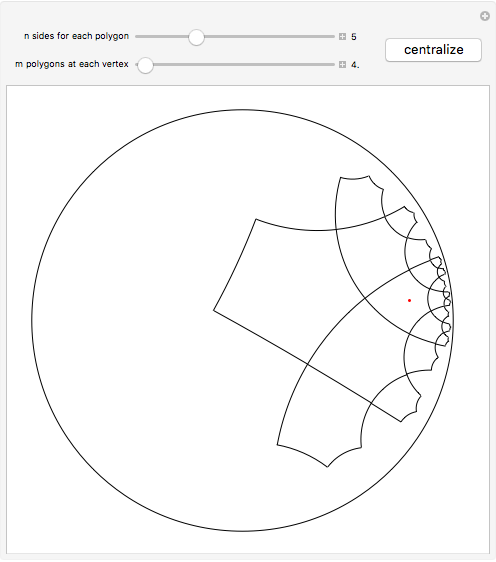
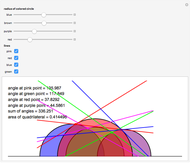
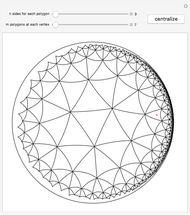
This Demonstration shows the beginning of the tiling of the hyperbolic plane (in the Poincaré disk model) with regular 
-gons, 
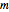of them touching at each vertex inside the tiling. (There may be fewer than 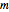polygons touching a vertex near the boundary of the current tiling.) Click the plane to change where the center appears.
Contributed by: Gašper Zadnik (March 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For every pair of positive integers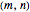 
satisfying 
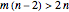, there is a tiling of the hyperbolic plane with regular -gons such that 
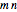-gons touch at each vertex. Since isometries of the hyperbolic plane act transitively on it, the center of the "initial" -gon (from which we start the tiling) can be chosen anywhere in the hyperbolic plane.
Reference
[1] Wikipedia. "Uniform Tilings in Hyperbolic Plane." (Mar 1, 2013) en.wikipedia.org/wiki/Uniform_tilings_in _hyperbolic _plane.
Permanent Citation
Reflecting a Regular Polygon across Its Sides in the Hyperbolic Plane
Gasper Zadnik
Poincaré Hyperbolic Disk
Eric W. Weisstein
The Disappearing Hyperbolic Squares
Stan Wagon
Hyperbolic Quadrilateral
Ron Grosz
Hyperbolic Triangle
Michael Rach and Ron Grosz
Regular Tilings
Karl Scherer
Recursively Defined Partial Tilings of the Plane
Enrique Zeleny
Direct Isometries of the Hyperbolic Plane
Gasper Zadnik
Tiling Constructor
Karl Scherer
Ammann Tiling A1
Dieter Steemann
