Regular Tilings

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
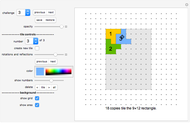
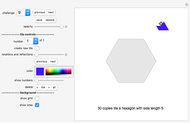
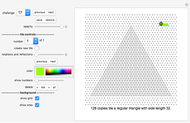
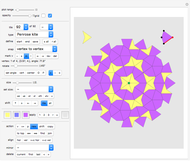
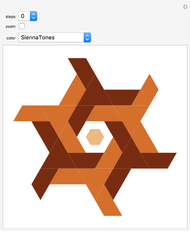
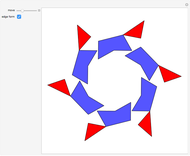
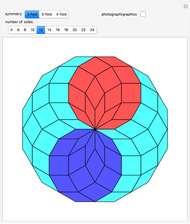
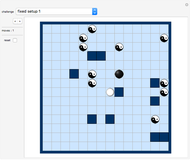
The do-it-yourself tilings shown in this Demonstration each use only one shape, and only one size of this shape.
[more]
Contributed by: Karl Scherer (May 2008)
Additional contributions by: David Klarner, Michael Reid andJaap Scherphuis
Open content licensed under CC BY-NC-SA
Snapshots
Details
Much of the material presented here has been taken from the book A Puzzling Journey to the Reptiles and Related Animals, privately published by the author in 1987.
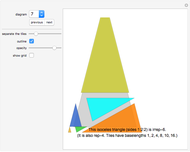
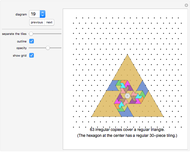
Many trivial and some very difficult tilings have been omitted. For each shape only one interesting tiling has been selected.
Some of the tilings, especially the odd tilings, are difficult to find (odd tilings have an odd number of tiles).
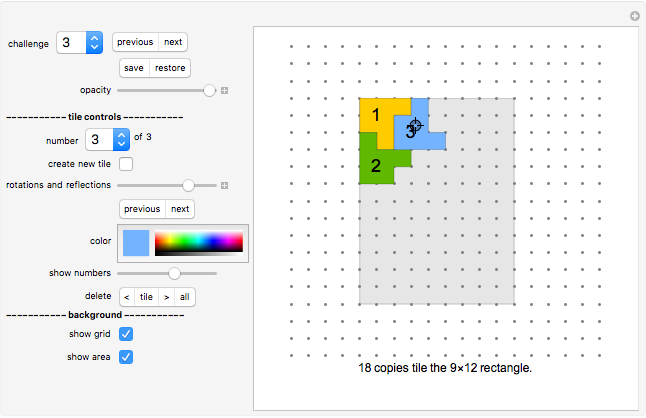
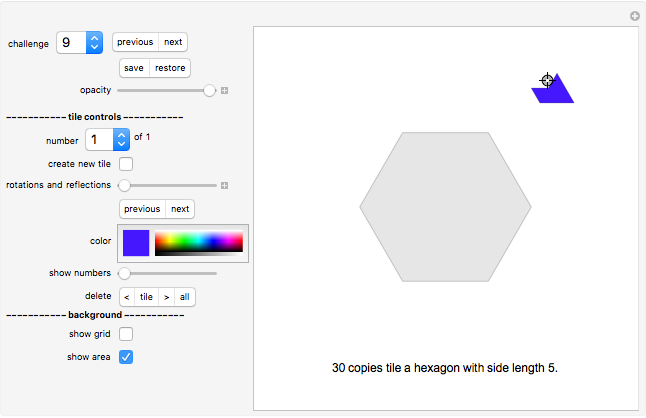
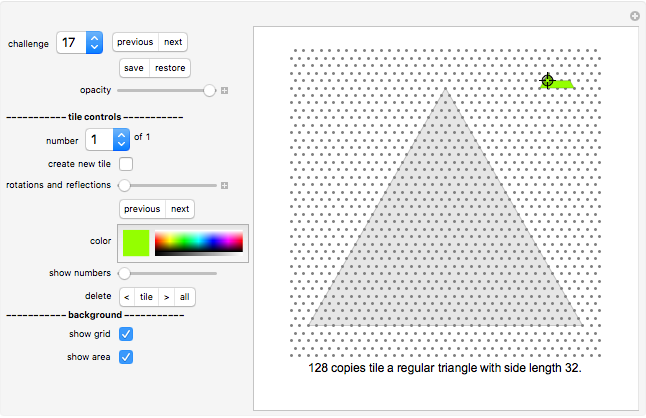
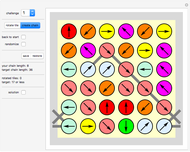
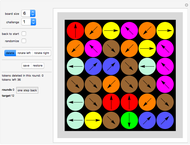
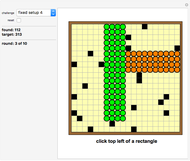
Do-It-Yourself tiling:
The challenge selection shows you various areas to fill and the tile to fill it with.
You draw a tile by a stamping method: Drag the tile with the Locator (cross hairs) to the desired position on the board.
Click the color selection to select the tile's color.
Use the "rotations and reflections" slider to select the orientation of the tile (or the "previous/next" SetterBar underneath it, which is often more convenient).
Once you are happy with the position and orientation of the tile, click "create new tile" button to create your next tile. The new tile will be displayed at the same position as the current tile. Move it to the side to see it separately.
You can select any tile number to make this tile the current one. (Use the "show numbers" slider to see the tile numbers.)
This Demonstration stores all setups you create. Hence you can come back to a half-solved challenge at any time.
You can also save and restore your intermediate solutions with the "save/restore" setter bar.
The "delete" setter bar:
Click "<" to delete all previous tiles. Click "tile" to delete the current tile. Click ">" to delete all following tiles. Click "all" to delete all tiles (except the current one). Note that you can only use the "delete" options if more than one tile is left.
Contributions by other authors:
Jaap Scherphuis: found tiling 2 David Klarner: solution to problem 5. Michael Reid: solution to problems 11, 12, 13, and 15.
All other solutions were found by the author.
Permanent Citation
"Regular Tilings"
http://demonstrations.wolfram.com/RegularTilings/
Wolfram Demonstrations Project
Published: May 21 2008