Time Evolution of the Wavefunction in a 1D Infinite Square Well
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
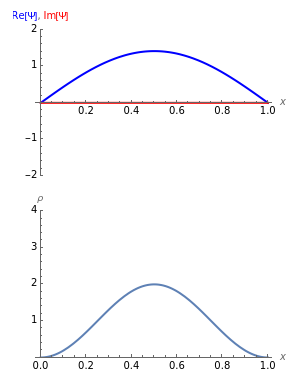
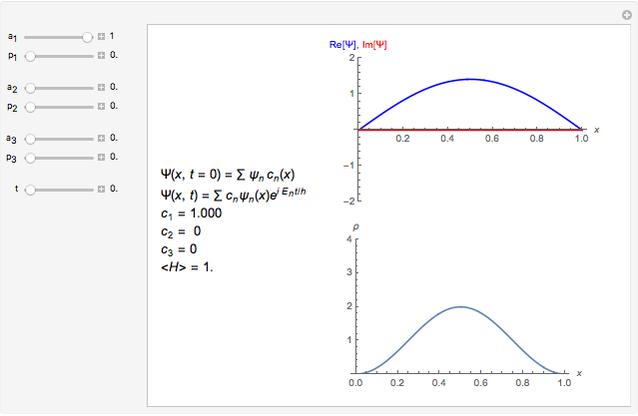
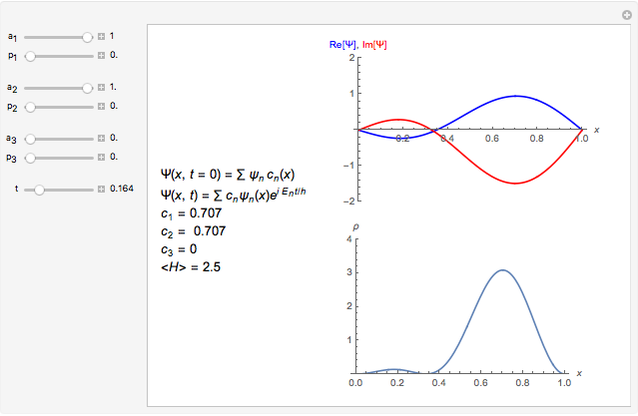
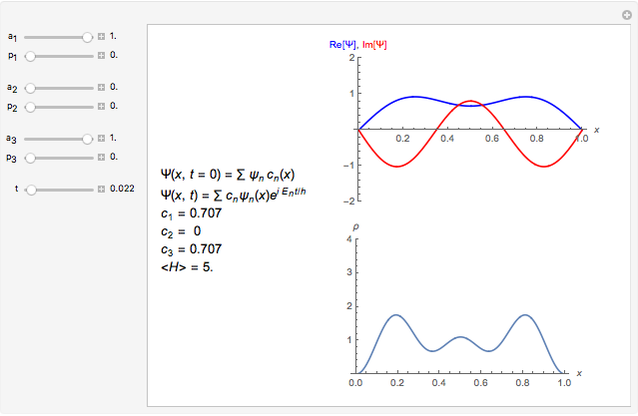
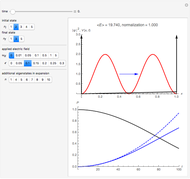
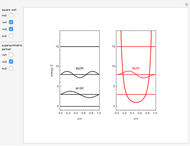
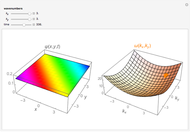
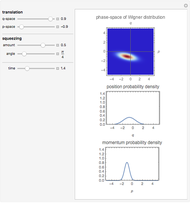
This Demonstration shows some solutions to the time-dependent Schrödinger equation for a 1D infinite square well. You can see how wavefunctions and probability densities evolve in time. You can set initial conditions as a linear combination of the first three energy eigenstates.
Contributed by: Jonathan Weinstein (June 2011)
(University of Nevada, Reno)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Vary the time 
to see the evolution of the wavefunction of a particle of mass 
in an infinite square well of length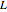 
. Initial conditions are a linear combination of the first three energy eigenstates 
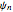. The amplitude of each coefficient is set by the 
sliders. The phase of each coefficient at 
is set by the 
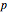sliders. The wavefunction is automatically normalized.
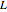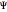Position is in units of .
is in units of 
.
is in units of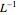 
.
Energy is in units of 
.
Time is in units of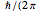
energy units).
Permanent Citation
Finite Potential Well
Michael R. Braunstein (Central Washington University)
Perturbed Infinite Square Well
Martha Takats
Time Evolution of a Quantum Free Particle in 1D
Porscha McRobbie and Eitan Geva
Quantum Particles in an Infinite Square Potential Well
Jeff Bryant
Harmonic Electric Field Applied to a Particle in an Infinite Square Well
James A. Miller
Particle in an Infinite Spherical Well
S. M. Blinder
Particle in an Infinite Circular Well
Enrique Zeleny
Supersymmetry for the Square-Well Potential
S. M. Blinder
Time Evolution of a Quantum Free Particle in 2D
Porscha McRobbie and Eitan Geva
Time Evolution of Squeezed Quantum States of the Harmonic Oscillator
Arkadiusz Jadczyk
