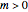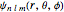Particle in an Infinite Spherical Well

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
A particle of mass 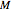 in an infinite spherical potential well of radius
in an infinite spherical potential well of radius 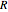 is described by the Schrödinger equation
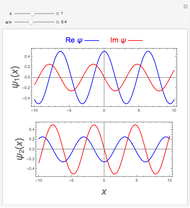
is described by the Schrödinger equation 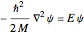 . The wavefunction is separable in spherical polar coordinates, such that
. The wavefunction is separable in spherical polar coordinates, such that 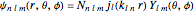 , where
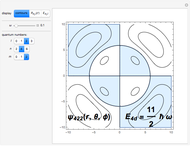
, where 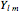 is a spherical harmonic,
is a spherical harmonic, 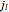 a spherical Bessel function, and
a spherical Bessel function, and  is a normalization constant. The boundary condition that
is a normalization constant. The boundary condition that  at
at 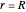 is fulfilled when
is fulfilled when  is the
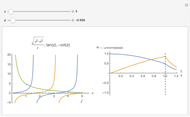
is the 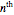 zero of the spherical Bessel function
zero of the spherical Bessel function 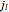 . The quantized energy levels are then given by
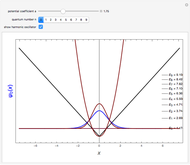
. The quantized energy levels are then given by 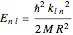 and are
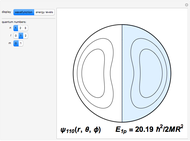
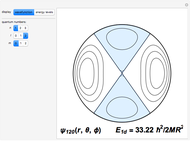
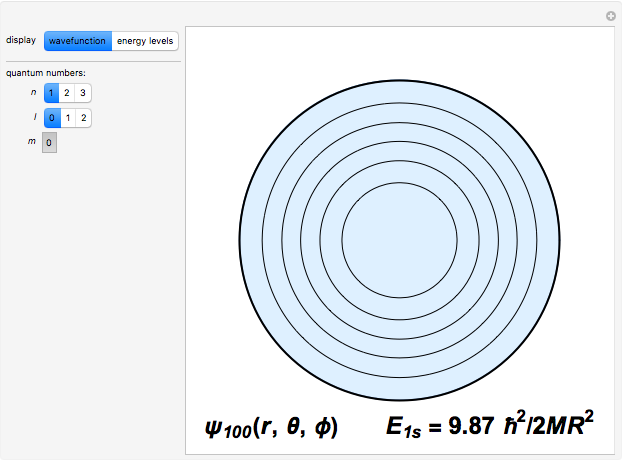
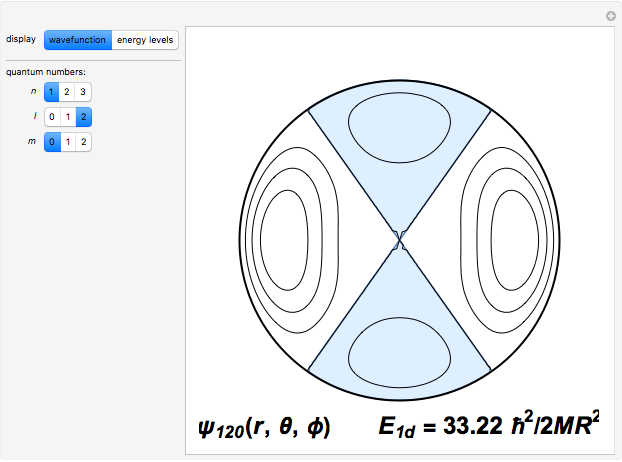
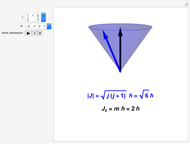
and are 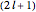 -fold degenerate with
-fold degenerate with  . The conventional code is used to label angular momentum states, with
. The conventional code is used to label angular momentum states, with 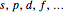 representing
representing 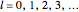 . Unlike atomic orbitals, the
. Unlike atomic orbitals, the 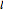 -values are not limited by
-values are not limited by  ; thus one will encounter states designated
; thus one will encounter states designated 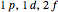 , etc.
, etc.
Contributed by: S. M. Blinder (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
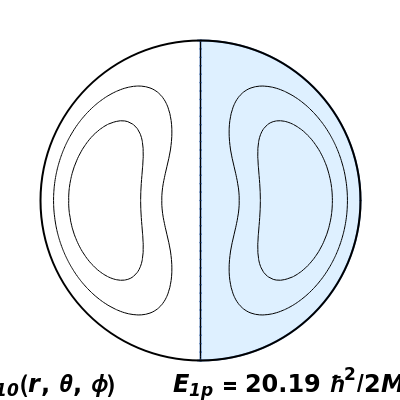
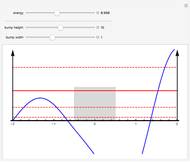
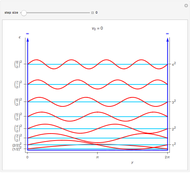
Snapshots 1–3: the three lowest energy states
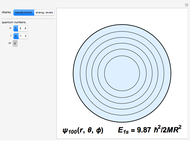
Snapshot 4: energy-level diagram
Permanent Citation