Tomahawk Quinsector

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
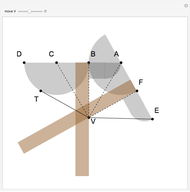
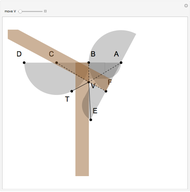
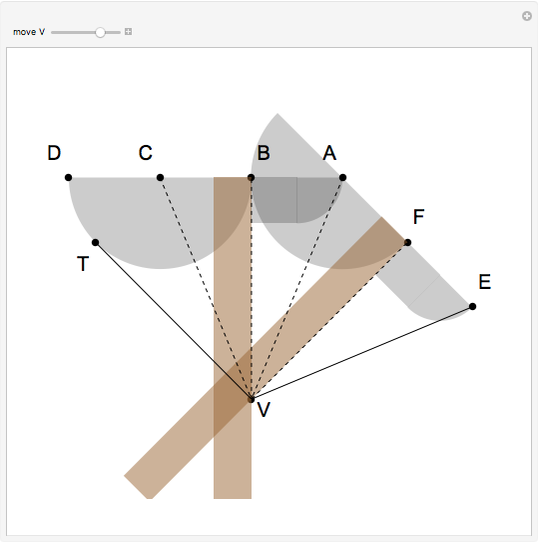
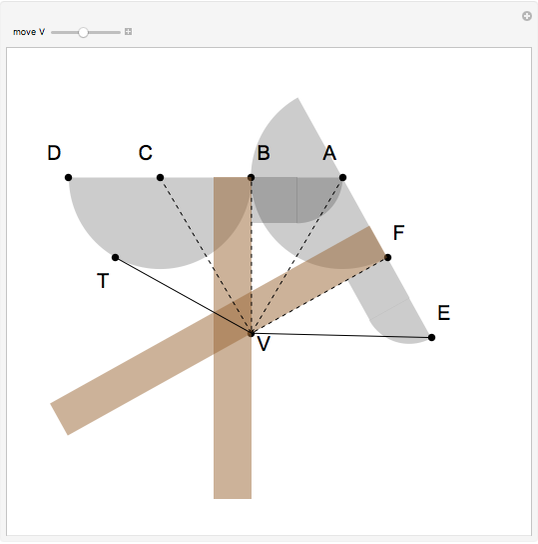
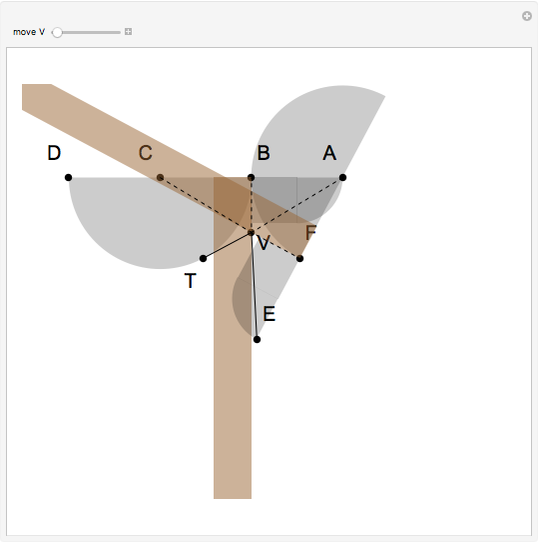
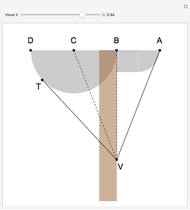
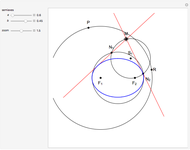
This Demonstration shows two attached tomahawks that form a quinsector, an instrument that divides an angle into five equal parts. In the figure, the angle  is quinsected. It is fairly easy to see that the five right triangles are congruent.
is quinsected. It is fairly easy to see that the five right triangles are congruent.
Contributed by: Izidor Hafner (December 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
To construct a tomahawk, see Tomahawk Trisection of an Angle.
Reference
[1] G. E. Martin, Geometric Constructions, New York: Springer, 1998 pp. 20–21.
Permanent Citation
"Tomahawk Quinsector"
http://demonstrations.wolfram.com/TomahawkQuinsector/
Wolfram Demonstrations Project
Published: December 4 2017