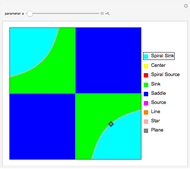
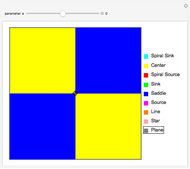
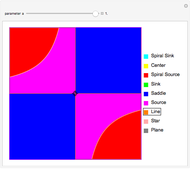
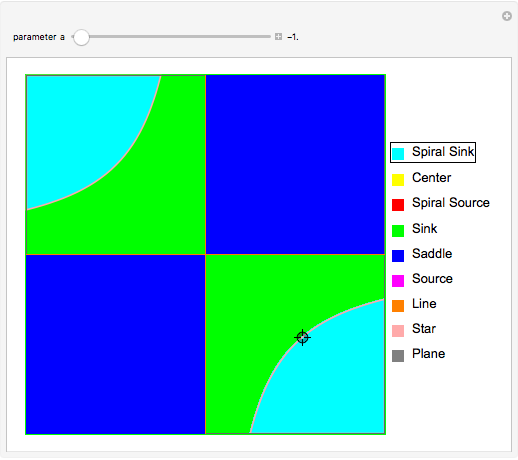
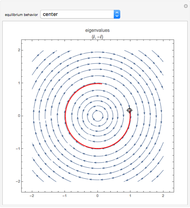
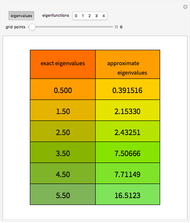
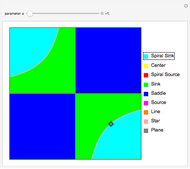
The stability of solutions of a linear system of differential equations with constant coefficients can be classified using the trace and determinant of the coefficient matrix, without having to solve the system. Here the system in question is of the form 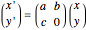, where , , and are real parameters. The stability of solutions of this system exhibit a bifurcation at , and solutions are qualitatively different depending on whethe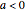r , , or 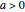. This Demonstration represents the stability of solutions in the 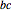-plane as varies. Drag the locator to identify the different regions.