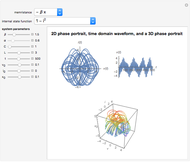
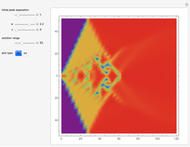
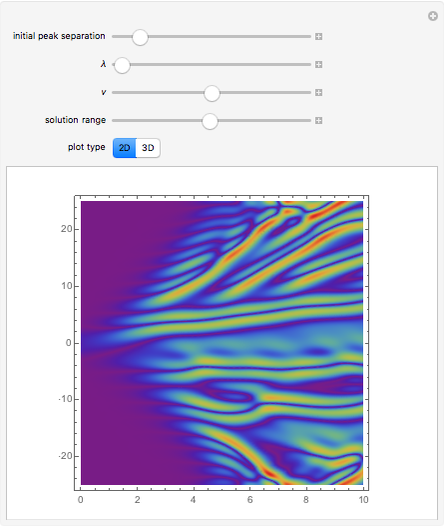
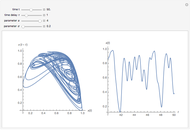
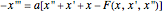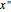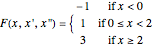A Third-Order Differential Equation with Chaotic Solutions
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
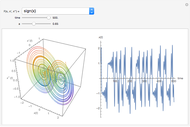
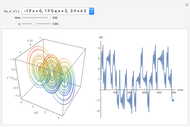
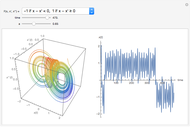
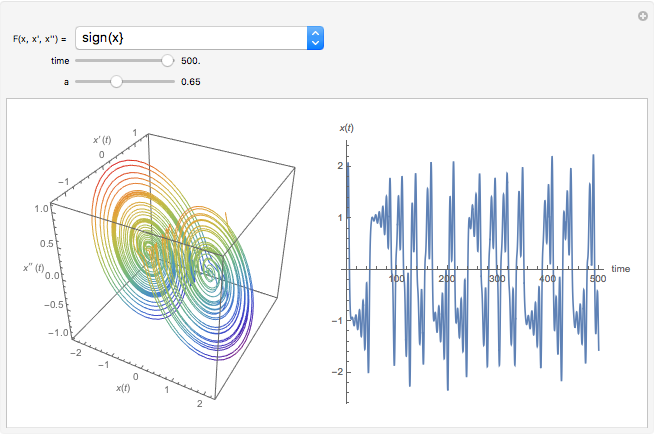
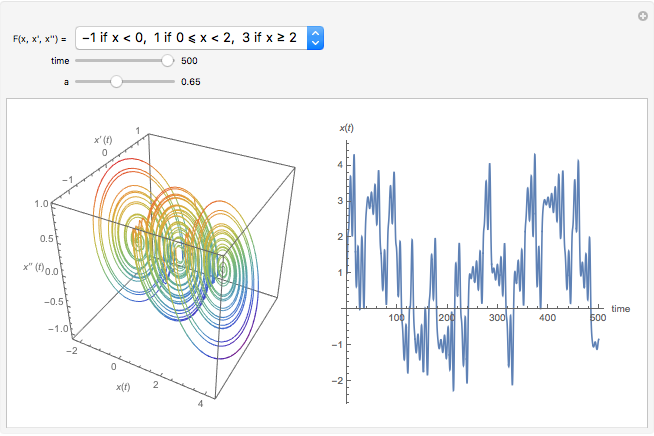
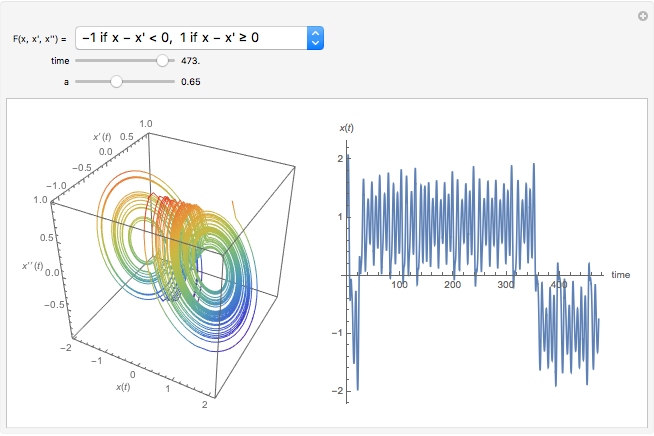
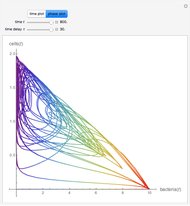
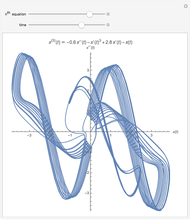
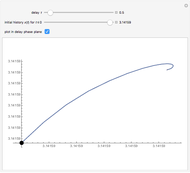
The solution of the following simple third-order ordinary differential equation exhibits chaos [1]:
[more]
Contributed by: Clay Gruesbeck (May 2013)
Open content licensed under CC BY-NC-SA
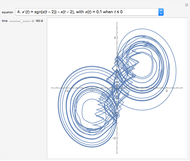
Snapshots
Details
Reference
[1] A. S. Elwakil, K. N. Salama, and M. P. Kennedy, "An Equation for Generating Chaos and Its Monolithic Implementation," International Journal of Bifurcation and Chaos, 12(12), 2002 pp. 2885–2895. doi:10.1142/S0218127402006205.
Permanent Citation