A Triangle Model of Criminality

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
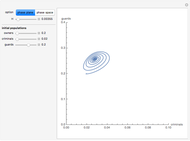
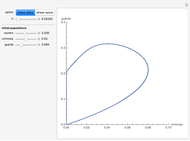
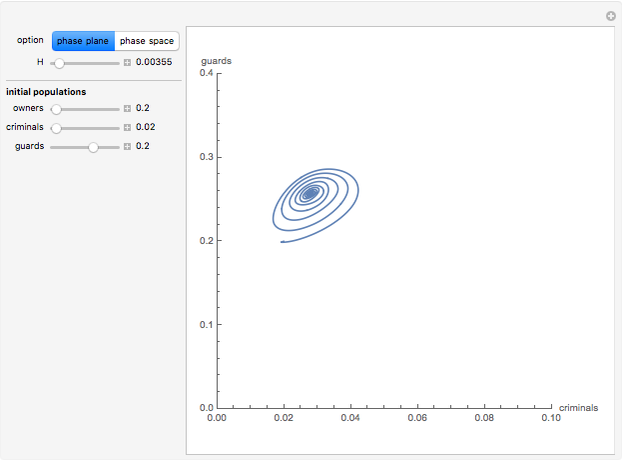
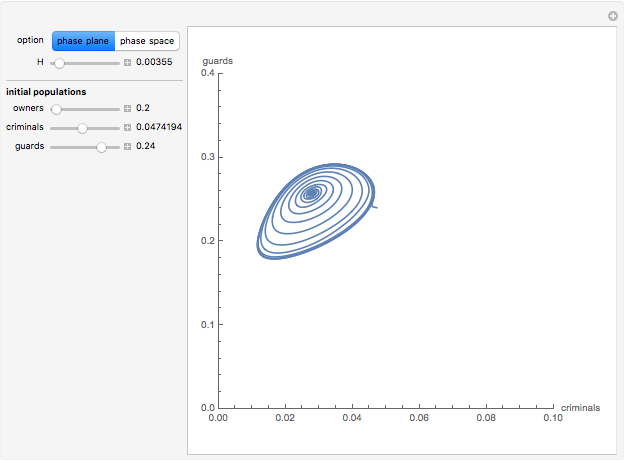
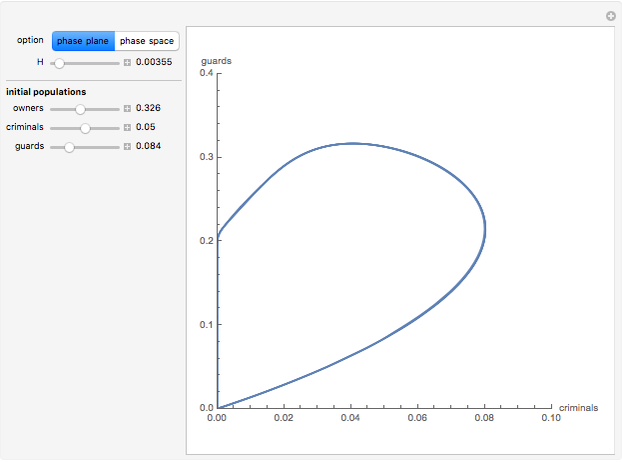
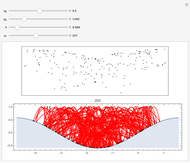
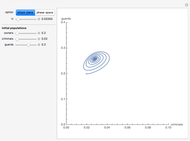
Consider a society divided into three classes: owners, criminals, and guards, in which two predators (criminals and security guards) compete for the same prey (owners). By tuning the efficiency 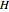 of the security guards, the behavior of this society varies, crossing several bifurcation points. Orbits can be drawn for different initial values of the population.
of the security guards, the behavior of this society varies, crossing several bifurcation points. Orbits can be drawn for different initial values of the population.
Contributed by: Silvia Pierazzini and Juan C. Nuño (March 2011)
After work by: Juan C. Nuño, Miguel A. Herrero, and Mario Primicerio
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let the populations of the owners, criminals, and guards be  ,
, 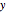 , and
, and  .
.
Consider a society in which the criminal rate is 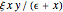 , where ξ is a proportionality constant, and the rate of arrests by guards is
, where ξ is a proportionality constant, and the rate of arrests by guards is 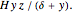
The equations that describe the model are:
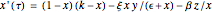 .
.
In the absence of criminals and guards, the population of owners obeys a logistic-type dynamic (with maximum capacity 1). The presence of criminals hinders the growth of  and the existence of security forces represents a cost for the owners.
and the existence of security forces represents a cost for the owners.
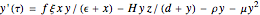 .
.
The criminal population increases at the rate 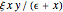 and it decreases because of the predatory action of guards, the retirement of criminals, and the interspecific competition of criminals (the quadratic last term).
and it decreases because of the predatory action of guards, the retirement of criminals, and the interspecific competition of criminals (the quadratic last term).
 .
.
The growth of the security forces is proportional to the crimes committed and decreases as a consequence of the casualties suffered in encounters with criminals and of natural decay.
For more details, see J. C. Nuño, M. A. Herrero, and M. Primicerio, "A Triangle Model of Criminality," Physica A, 387(12), 2008 pp. 2926–2936.
Permanent Citation