Triangle Side Length Inequality
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
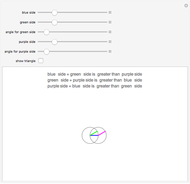
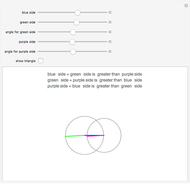
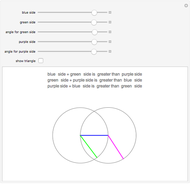
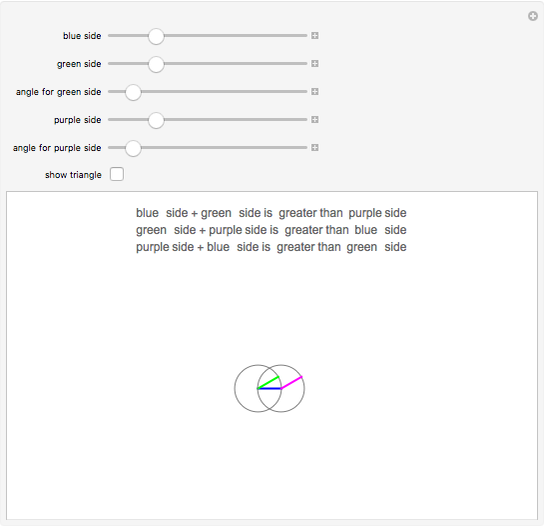
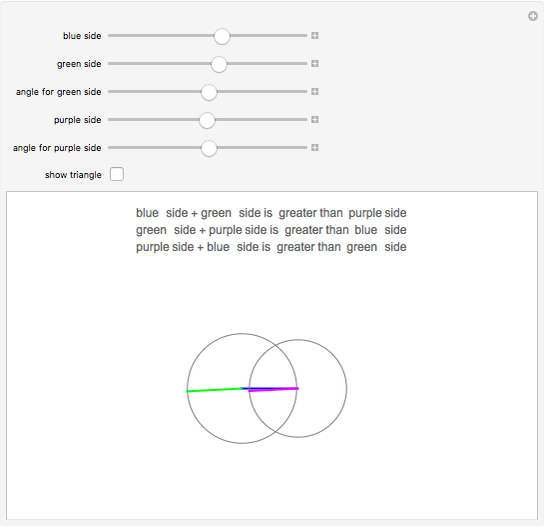
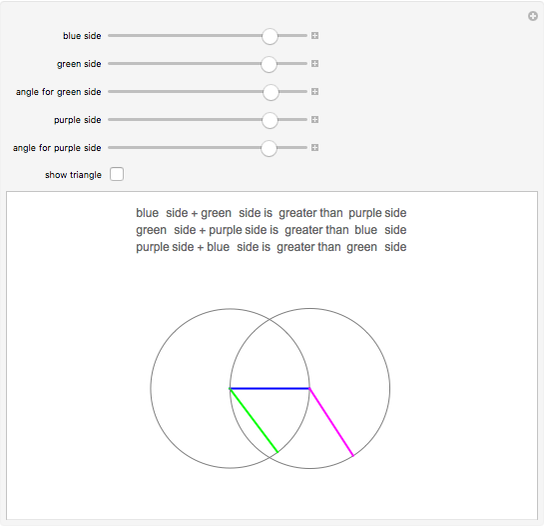
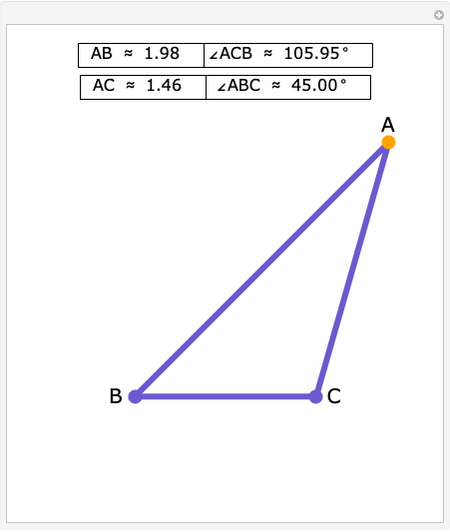
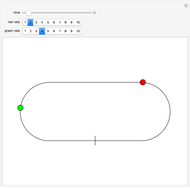
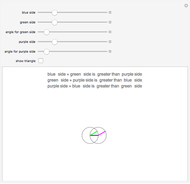
Three lines of given length can possibly form a triangle. If the sum of any two lengths is greater than the third length, a triangle can be formed. This is the case whenever the gray circles intersect.
Contributed by: Tom De Vries (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Triangle Side Length Inequality"
http://demonstrations.wolfram.com/TriangleSideLengthInequality/
Wolfram Demonstrations Project
Published: March 7 2011
15. Construct a Triangle Given the Lengths of Two Sides and the Median to the Third Side
Izidor Hafner
7. Construct a Triangle Given the Lengths of Two Sides and a Median of the Third Side
Izidor Hafner
27b. Construct a Triangle Given Its Perimeter, an Angle and the Length of the Altitude to the Side Opposite the Angle
Izidor Hafner
27a. Construct a Triangle Given a Side, the Length of the Altitude to It and the Opposite Angle
Izidor Hafner
Side-Splitting Triangle Ratios
Ed Pegg Jr
Side Lengths Opposite Unequal Angles
Jay Warendorff
8. Construct a Triangle Given the Lengths of Two Sides and the Length of the Altitude to One of Them
Izidor Hafner
30. Construct a Triangle ABC Given the Length of AB, the Angle at C and the Difference of the Other Two Sides
Izidor Hafner
28. Construct a Triangle ABC Given the Length of AB, the Sum of the Other Two Sides, and a Line Containing C
Marko Razpet and Izidor Hafner
A Triangle Inequality Involving the Altitudes, Semiperimeter, Inradius, and Circumradius
Jay Warendorff
