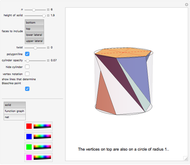
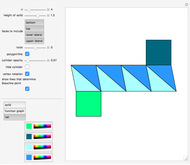
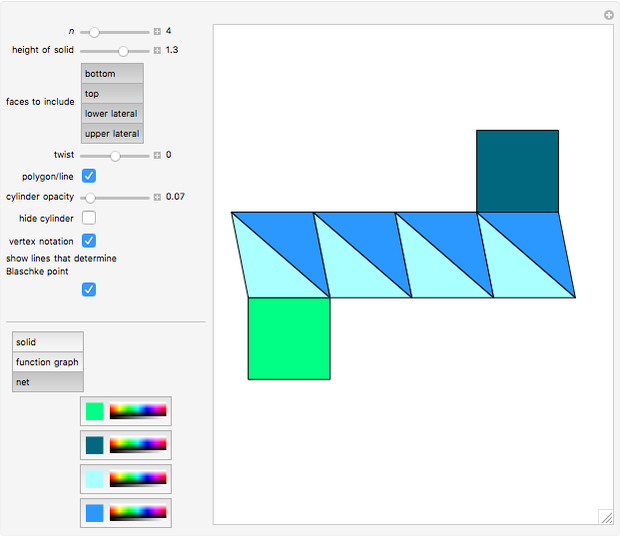
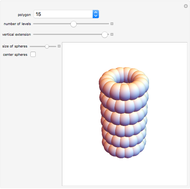
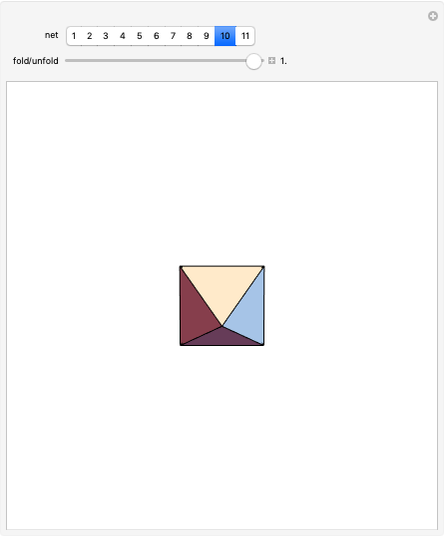
Twisted Antiprism

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
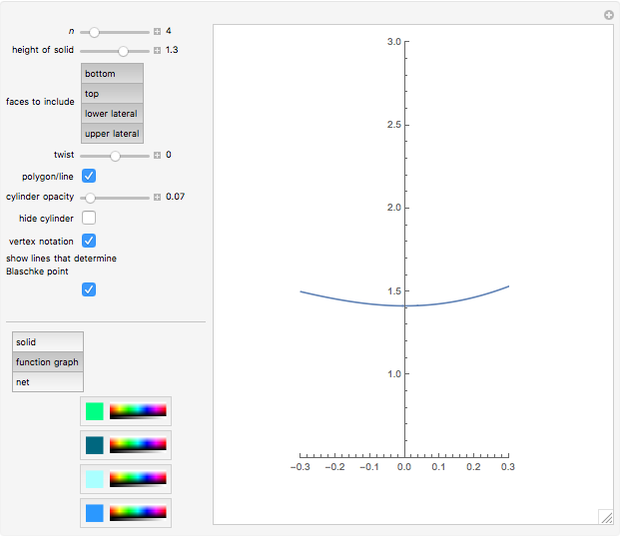
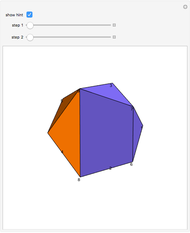
A twisted antiprism is obtained from an antiprism by rotating its top face by 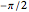 or
or  ; it has a nontrivial infinitesimal isometric deformation. The case of the twisted triangular antiprism is known as Wunderlich's (or Schoenhardt's) octahedron. According to the Blaschke–Liebmann theorem, four nonadjacent faces of an infinitesimally flexible octahedron meet at a point. It seems that the theorem can be extended to the twisted antiprisms.
; it has a nontrivial infinitesimal isometric deformation. The case of the twisted triangular antiprism is known as Wunderlich's (or Schoenhardt's) octahedron. According to the Blaschke–Liebmann theorem, four nonadjacent faces of an infinitesimally flexible octahedron meet at a point. It seems that the theorem can be extended to the twisted antiprisms.
Contributed by: Izidor Hafner (August 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Let 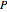 be a polyhedron with triangular faces and vertex set
be a polyhedron with triangular faces and vertex set 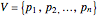 . An infinitesimal isometric deformation of
. An infinitesimal isometric deformation of 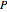 is a map
is a map 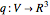 such that
such that
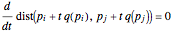 at
at 
for all edges 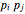 of
of 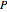 [3, definition 2.1].
[3, definition 2.1].
This condition is equivalent to 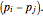
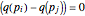 .
.
A polyhedron is infinitesimally flexible if it has an infinitesimal isometric deformation in which some of its dihedral angles change.
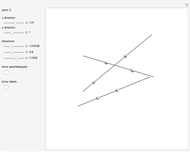
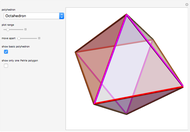
A theorem of Blaschke and Liebmann states: Let 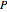 be a polyhedron combinatorially isomorphic to the octahedron. Color the faces of
be a polyhedron combinatorially isomorphic to the octahedron. Color the faces of 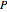 black and white so that each pair of adjacent faces has different colors. Then
black and white so that each pair of adjacent faces has different colors. Then 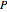 is infinitesimally flexible if and only if the four black faces intersect at a point, or equivalently, if the four white faces intersect at a point. The intersection points can lie at infinity [3, theorem 2.8].
is infinitesimally flexible if and only if the four black faces intersect at a point, or equivalently, if the four white faces intersect at a point. The intersection points can lie at infinity [3, theorem 2.8].
The polyhedron is the simplest nonconvex polyhedron that cannot be triangulated into tetrahedra without adding new vertices [4].
References
[1] P. R. Cromwell, Polyhedra, Cambridge: Cambridge University Press, 1997 pp. 222–223.
[2] M. Goldberg, "Unstable Polyhedral Structures," Mathematics Magazine, 51, 1978 pp. 165–170.
[3] I. Izmestiev, "Examples of infinitesimally Flexible 3-dimensional Hyperbolic Cone-Manifolds," Journal of the Mathematical Society of Japan, 63(2), 2011 pp. 363–713. projecteuclid.org/euclid.jmsj/1303737798.
[4] Wikipedia. "Schönhardt polyhedron." (May 27, 2016) en.wikipedia.org/wiki/Sch%C3%B6nhardt_polyhedron.
Permanent Citation