Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Typical Wavefronts in 2D and 3D

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

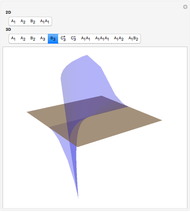
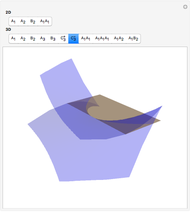
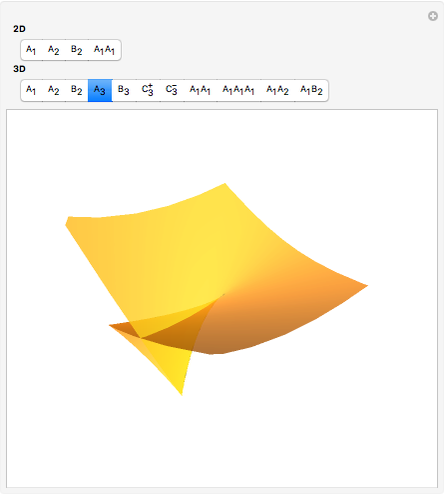
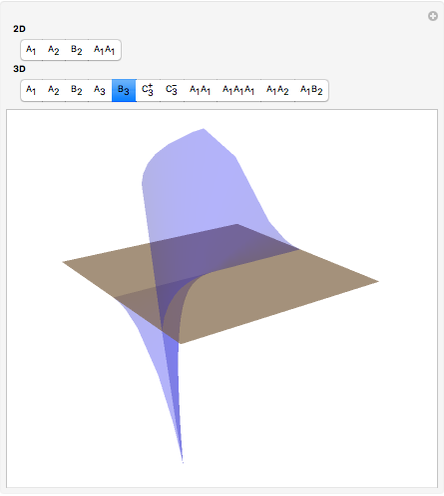
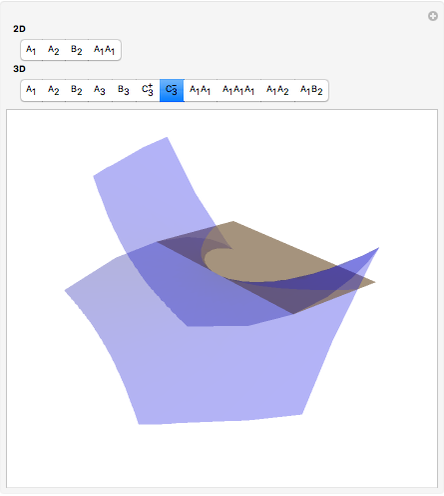
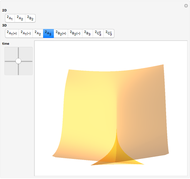
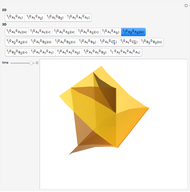
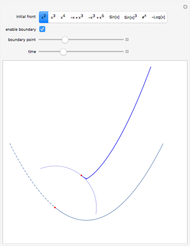
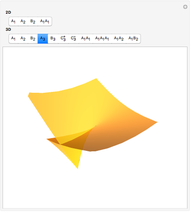
This Demonstration shows all "generic" wavefronts and boundary wavefronts in the 2D plane and in 3D space. It also shows all generic intersections of such wavefronts. You can observe their shapes from any direction by rotating the 3D images, which will help your understanding of the structure of generic wavefronts.

Contributed by: Takaharu Tsukada (March 2010)
Open content licensed under CC BY-NC-SA

Snapshots

Details

, .

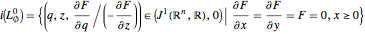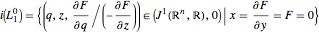Then the wavefronts of 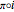are given by

.

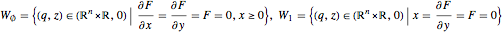You can observe behaviors of wavefronts in a plane in Bifurcation of Boundary Wavefronts for Some Graphs.

In the case :

In the case :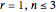

References

[1] V. I. Arnold, Singularities of Caustics and Wave Fronts, Dordrecht: Kluwer Academic Publishers, 1990.

[2] V. I. Arnold, S. M. Gusein–Zade, and A. N. Varchenko, Singularities of Differential Maps I, Basel: Birkhäuser, 1985.

[3] T. Tsukada, "Genericity of Caustics and Wavefronts on an r-Corner", 14(3), The Asian Journal of Mathematics, 2010 pp. 335–358.

[4] T. Tsukada, "Bifurcations of Wavefronts on r-Corners: Semi-Local Classification," 18(3) Methods and Applications of Analysis, 2011 pp. 303–334.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send