Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

The Four-Vertex Theorem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

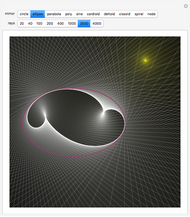
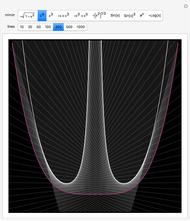
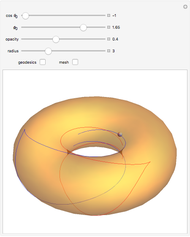
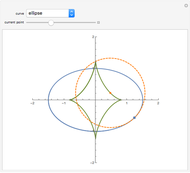
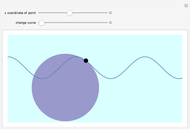
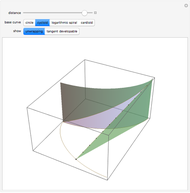
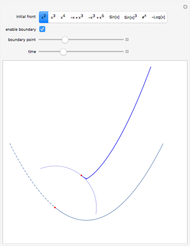
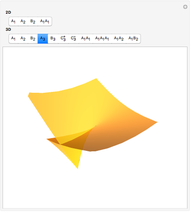
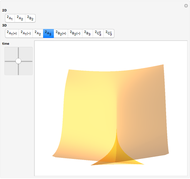
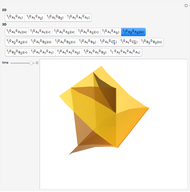
This shows the result of the four-vertex theorem: A simple closed curve has at least four vertices. You can transform the closed curve by dragging the locator. If the caustic extends beyond the window, you can reduce its size.

[more]

Let be a smooth plane curve parametrized by arc length , that is, for all . The number is called the curvature of at . A vertex of is a point where . A vertex corresponds to a cusp of the caustic generated by the curve. The theorem implies that the caustic of a general simple closed curce has at least four cusps (for a caustic, see Caustics on Spline Curves).

[less]

Contributed by: Takaharu Tsukada (January 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Manfredo P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice Hall, 1976.

Ian R. Porteous, Geometric Differentiation: For the Intelligence of Curves and Surfaces, Cambridge University Press, 1994.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send