Catastrophe Set of the Plane Projection of a Movable Surface

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
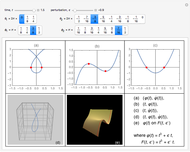
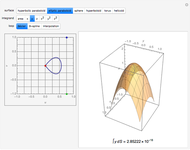
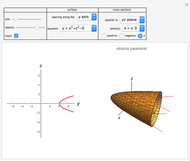
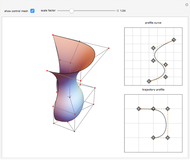
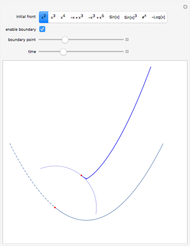
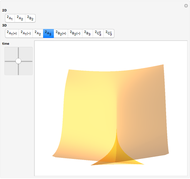
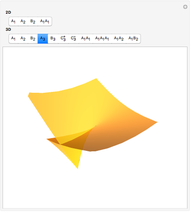
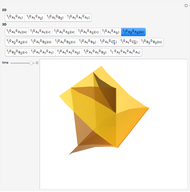
This Demonstration shows the catastrophe set of the plane projection from the surface. You can rotate the surface by dragging the locator. Observe that the cusp type is the only shape that appears for the catastrophe sets.
[more]
Contributed by: Takaharu Tsukada (February 2010)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The theory of Catastrophe Set of the Plane Projection of a Movable Surface in [1] and [2].
References
[1] V. I. Arnold, S. M. Gusein–Zade, and A. N. Varchenko, Singularities of Differentiable Maps, Vol. 1, Boston: Birkhäuser, 1985.
[2] T. Bröcker, Differentiable Germs and Catastrophes, London: Cambridge University Press, 1975.
[3] Author's page
Permanent Citation
"Catastrophe Set of the Plane Projection of a Movable Surface"
http://demonstrations.wolfram.com/CatastropheSetOfThePlaneProjectionOfAMovableSurface/
Wolfram Demonstrations Project
Published: February 23 2010