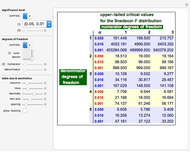
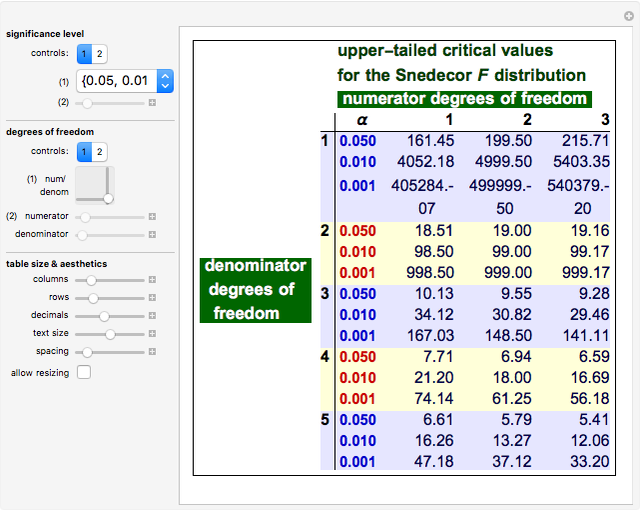
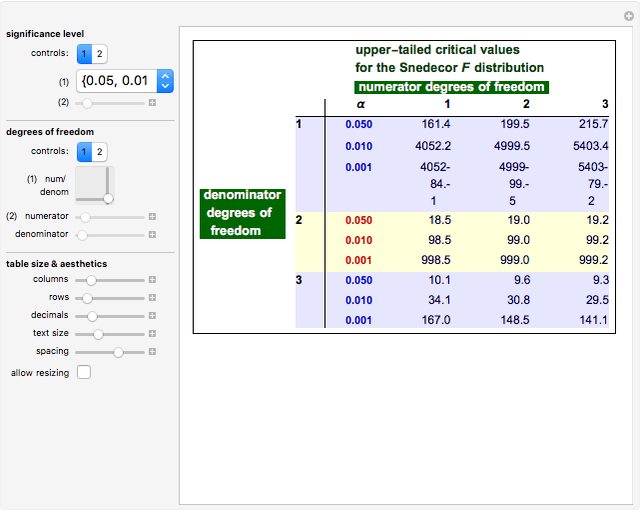
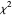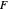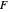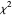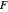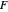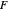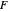Upper-Tailed Critical Values of the Fisher-Snedecor Distribution

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
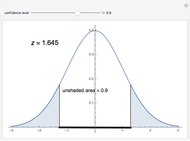
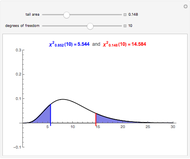
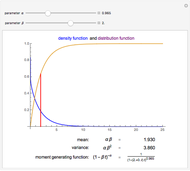
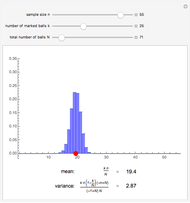
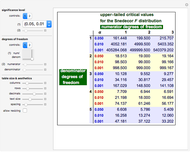
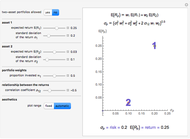
The 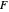 distribution of modern statistics (also called the
distribution of modern statistics (also called the  -ratio or Fisher-Snedecor or Snedecor's
-ratio or Fisher-Snedecor or Snedecor's 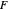 distribution) is a two-parameter continuous probability distribution arising out of the ratio of pairs of
distribution) is a two-parameter continuous probability distribution arising out of the ratio of pairs of  random variables, each divided by its own degrees of freedom. The
random variables, each divided by its own degrees of freedom. The  distribution plays a very prominent role in classical hypothesis testing in econometrics and statistics as the null distribution of the test statistic in tests of overall model significance and tests of joint linear restrictions generally, in the analysis of variance, and in likelihood-ratio tests.
distribution plays a very prominent role in classical hypothesis testing in econometrics and statistics as the null distribution of the test statistic in tests of overall model significance and tests of joint linear restrictions generally, in the analysis of variance, and in likelihood-ratio tests.
Contributed by: Jim R Larkin (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
A.C. Darnell, A Dictionary of Econometrics, Brookfield, VT: Edward Elgar Publishing, 1994.
D. B. Owen, Handbook of Statistical Tables, Reading, MA: Addison-Wesley Publishing Company, 1962.
M. Trott, The Mathematica GuideBook for Programming, New York: Springer-Verlag, 2004.
Permanent Citation