Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

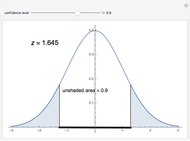
Critical Value z* for z-Scores for Confidence Levels

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

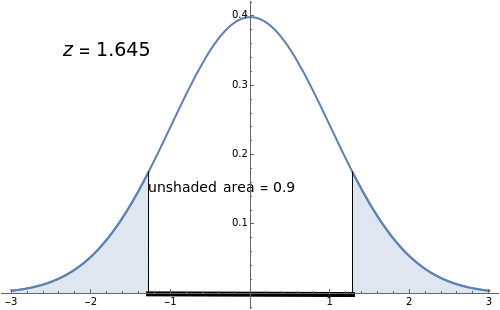
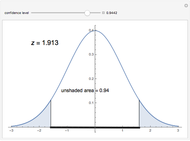
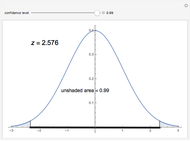
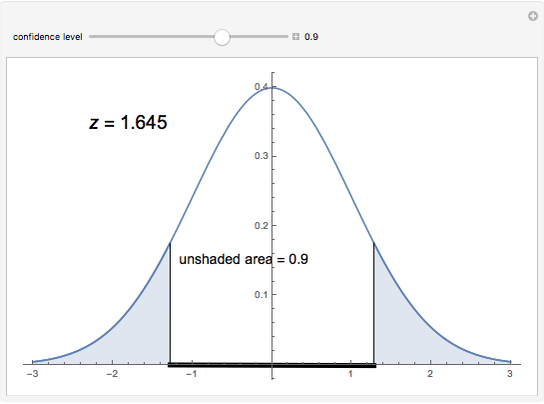
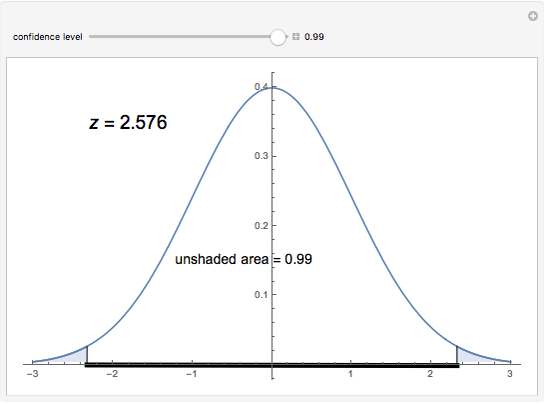
This Demonstration explains how a 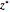-score (a critical -score) is related to confidence levels and used for the traditional method of significance tests [1]. As you move the slider, the confidence level changes, and in turn the area as well as the 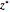-score changes.

[more]

The critical value is calculated by using a confidence level and finding the tail area of one side, and then taking the inverse of the cumulative distribution function of that area to get . A confidence interval is a range that is calculated using the sample mean and the population standard deviation. If many samples are taken and many intervals are created, of the resulting intervals will contain the true population mean, where is the chosen confidence level (for example, 99%).

[less]

Contributed by: Emily Hou and Esha Madhekar (May 2017)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This was a project for Advanced Topics in Mathematics II, 2016–2017, Torrey Pines High School, San Diego, CA.

References

[1] Armstrong State University, Department of Mathematics. "Critical Values of ." (Apr 28, 2017) www.math.armstrong.edu/statsonline/5/5.3.2.html.

[1] “InverseCDF” from Wolfram Language Documentation—A Wolfram Web Resource. reference.wolfram.com/language/ref/InverseCDF.html?q=InverseCDF.

[2] “NormalDistribution” from Wolfram Language Documentation—A Wolfram Web Resource. reference.wolfram.com/language/ref/NormalDistribution.html?q=NormalDistribution.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send