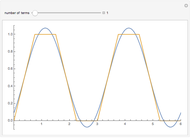
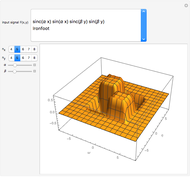
XFT2D: A 2D Fast Fourier Transform
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
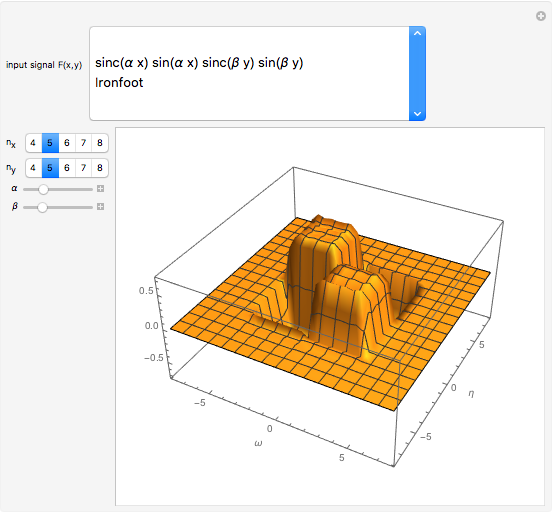
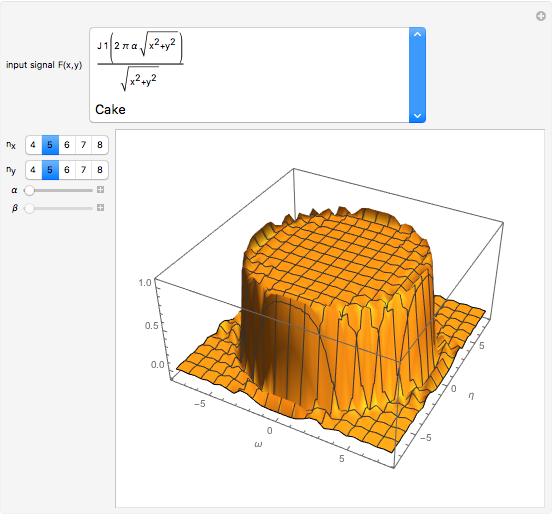
This Demonstration computes the real part of a two-dimensional fast Fourier transform that we call XFT2D to distinguish it from the usual FFT algorithms. It displays the transformed data points joined without any interpolation. XFT2D consists of a Kronecker product of two one-dimensional XFTs, one in each of the 
, 
directions. It approximates the two-dimensional Fourier transform defined as 
evaluated at the points 
, 
, 
, with 
and 
. The XFT is an improvement of the standard FFT (see the Details section).
Contributed by: Rafael G. Campos, J. Jesus Rico Melgoza, and Edgar Chavez (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The XFT is a discrete fractional Fourier transform that was obtained in closed form in [1] by using finite-dimensional vectors representing Hermite functions and some asymptotic properties of the Hermite polynomials. The XFT is given by the product 
, where 
is a diagonal matrix with 
diagonal element given by 
, 
, 
is the standard discrete Fourier transform, and 
. The XFT2D can be defined by the Kronecker product 
. The XFT is computed with and points in the and directions, respectively. The XFT is as fast as the FFT algorithm used to compute the discrete Fourier transform, but the output of the XFT is more accurate than the output of the FFT because it comes from an algorithm to compute the fast fractional Fourier transform based on a convergent quadrature formula.
[1] R. G. Campos, J. Rico–Melgoza, and E. Chavez, "XFT: Extending the Digital Application of the Fourier Transform," arXiv, 2009.
[2] R. G. Campos, J. Rico–Melgoza, and E. Chavez, "RFT: A Fast Discrete Fractional Fourier Transform," submitted.
Permanent Citation
XFT: An Improved Fast Fourier Transform
Rafael G. Campos, J. Jesus Rico Melgoza, and Edgar Chavez
Numerical Approximation of the Fourier Transform by the Fast Fourier Transform (FFT) Algorithm
Blazej Radzimirski
Fourier Transform Pairs
Porscha McRobbie and Eitan Geva
Rectangular Pulse and Its Fourier Transform
Nasser M. Abbasi
Fourier Series of Simple Functions
Alain Goriely
Amplitude and Phase in 2D Fourier Transforms
Katherine Rosenfeld
Fractional Fourier Transform
Enrique Zeleny
From Continuous- to Discrete-Time Fourier Transform by Sampling Method
Nasser M. Abbasi
Discrete Fourier Sine and Cosine Transforms
Daniel de Souza Carvalho
Pulse Fourier Approximation
Eric Mockensturm
