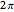From Continuous- to Discrete-Time Fourier Transform by Sampling Method

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
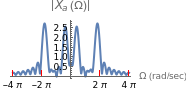
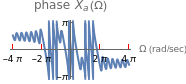
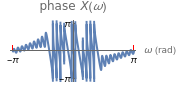
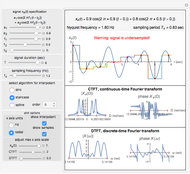
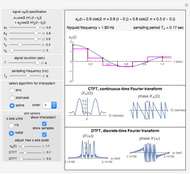
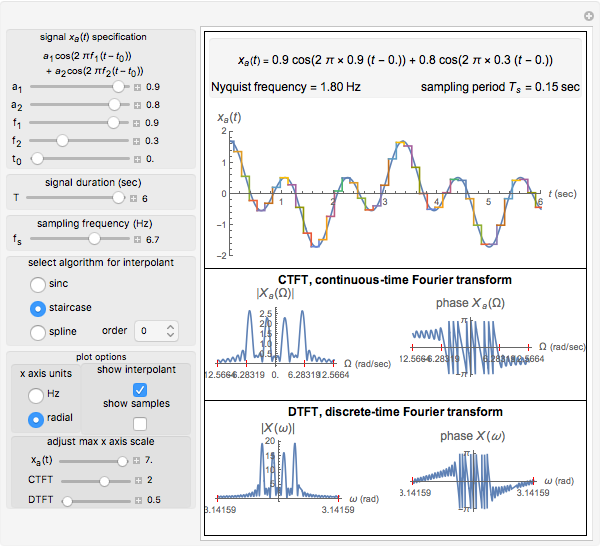
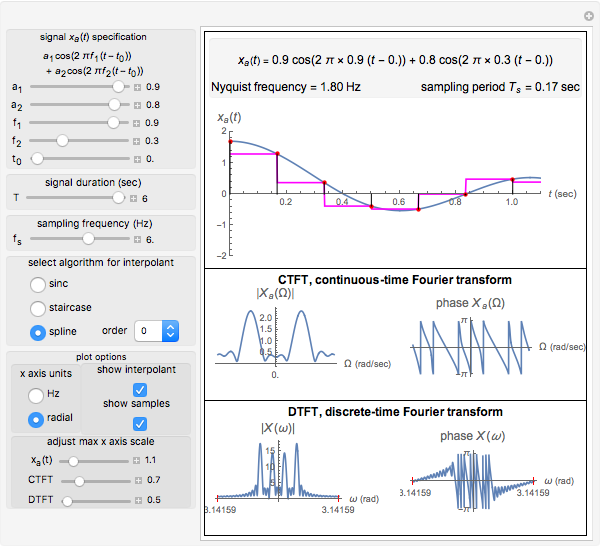
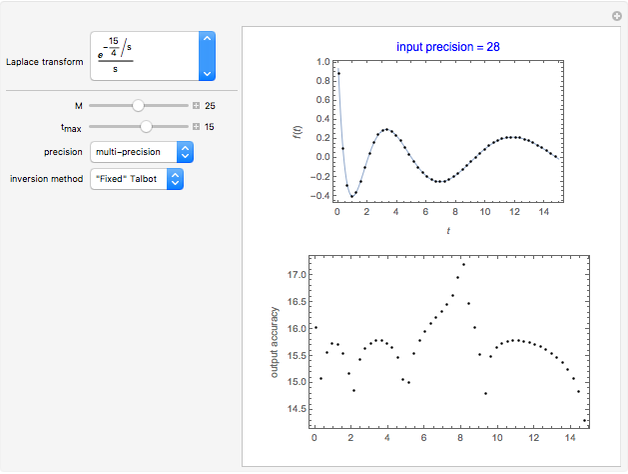
The purpose of this Demonstration is to show the relation between the continuous-time Fourier transform (CTFT) of a signal 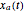 and the corresponding discrete-time Fourier transform (DTFT) of the signal
and the corresponding discrete-time Fourier transform (DTFT) of the signal 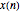 generated from
generated from 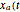 ) by sampling.
) by sampling.
Contributed by: Nasser M. Abbasi (March 2011)
Open content licensed under CC BY-NC-SA
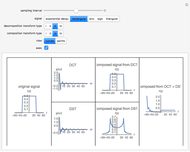
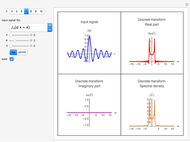
Snapshots
Details
The CTFT of a continuous time signal 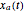 is defined as
is defined as 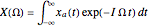 , where
, where  is in radians per second. The DTFT of a discrete signal
is in radians per second. The DTFT of a discrete signal 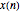 is defined as
is defined as  , where
, where  is in radians. In Mathematica, the built-in function FourierTransform implements the CTFT and the function FourierSequenceTransform implements the DTFT.
is in radians. In Mathematica, the built-in function FourierTransform implements the CTFT and the function FourierSequenceTransform implements the DTFT.
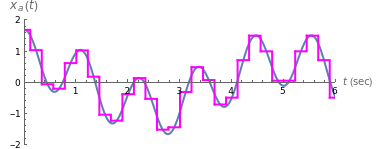
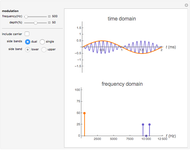
In this Demonstration, a signal 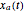 made up of two harmonics is used to analyze the process of sampling and generating the DTFT. The signal is given by
made up of two harmonics is used to analyze the process of sampling and generating the DTFT. The signal is given by 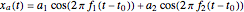 , where
, where 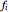 is the frequency of each harmonic in cycles per second (Hz),
is the frequency of each harmonic in cycles per second (Hz), 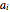 is the amplitude of each harmonic in units appropriate to the nature of the signal (such as volts), and
is the amplitude of each harmonic in units appropriate to the nature of the signal (such as volts), and 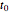 is the delay in seconds. The signal
is the delay in seconds. The signal 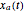 is of limited duration, which you can vary. Since
is of limited duration, which you can vary. Since 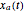 is time-limited, its spectrum will not be band-limited. In practice, this is handled by passing the signal through an antialiasing filter before sampling it. This filter has not been implemented in this Demonstration, thus some aliasing will be present even if the sampling frequency is greater than the Nyquist frequency. For the purposes of this Demonstration, it was not necessary to implement an antialiasing filter before sampling.
is time-limited, its spectrum will not be band-limited. In practice, this is handled by passing the signal through an antialiasing filter before sampling it. This filter has not been implemented in this Demonstration, thus some aliasing will be present even if the sampling frequency is greater than the Nyquist frequency. For the purposes of this Demonstration, it was not necessary to implement an antialiasing filter before sampling.
To reconstruct the time domain signal from the discrete time signal, one of the following algorithms can be selected: sinc interpolation, staircase interpolation, or spline interpolation (of order up to four). It was found that to obtain good reconstruction using the staircase and spline algorithms, the sampling frequency needs to be much higher than the Nyquist frequency.
You can vary the  axis plot range to see more details in the plot. Other plotting options are available to allow the change of units of the spectrum from Hz to radians and to superimpose the samples and the reconstructed signal on top of the original signal
axis plot range to see more details in the plot. Other plotting options are available to allow the change of units of the spectrum from Hz to radians and to superimpose the samples and the reconstructed signal on top of the original signal 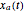 . This will show the effect of sampling.
. This will show the effect of sampling.
To reduce the signal 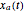 to one harmonic only, you can set the amplitude of the other harmonic to zero. For a constant (DC) signal
to one harmonic only, you can set the amplitude of the other harmonic to zero. For a constant (DC) signal 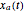 , you can set the frequencies
, you can set the frequencies 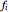 of both harmonics to zero.
of both harmonics to zero.
Permanent Citation