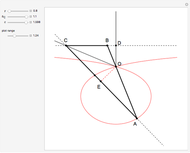
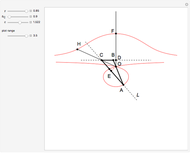
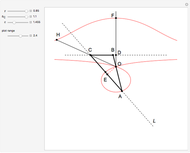
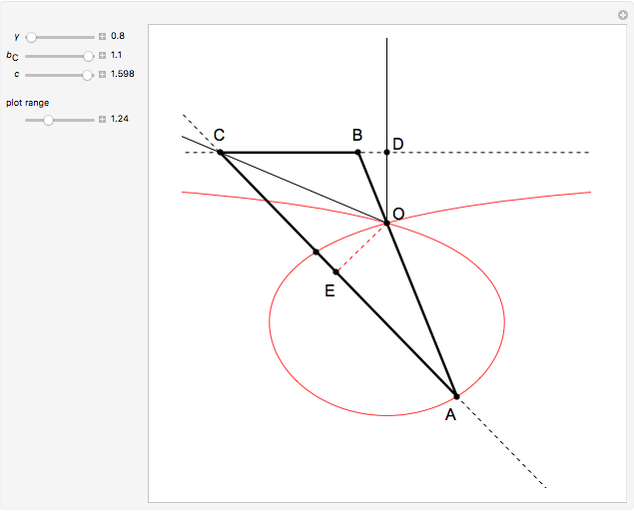
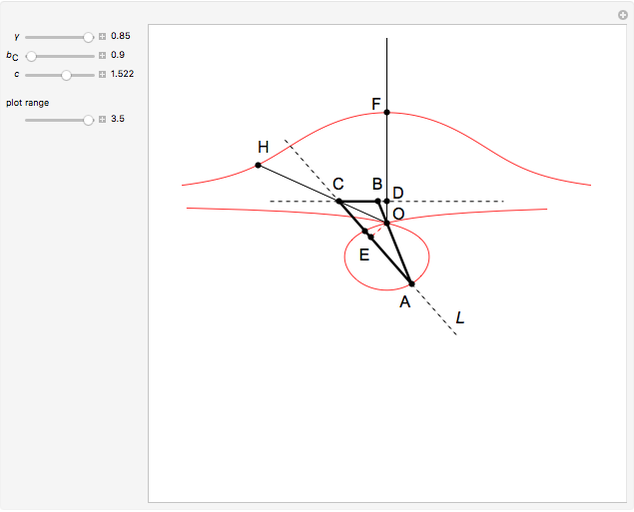
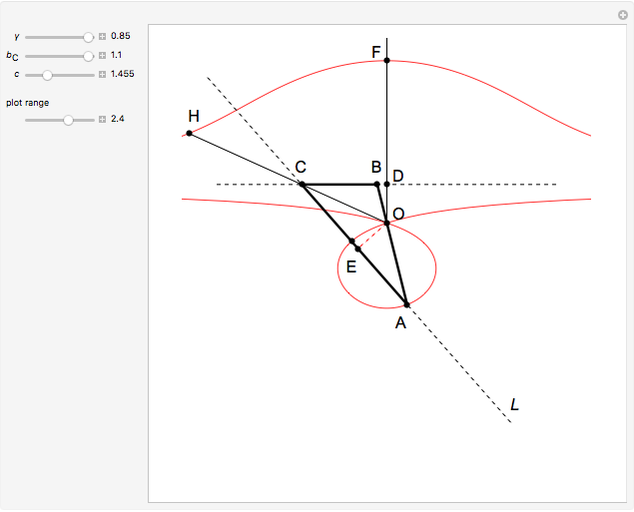
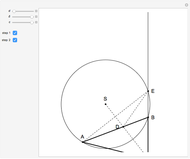
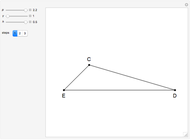
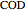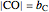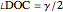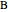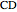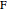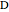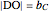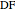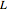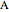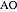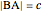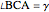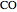26c. Construct a Triangle Given the Length of Its Base, the Angle Opposite the Base and the Length of That Angle's Bisector

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
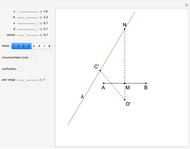
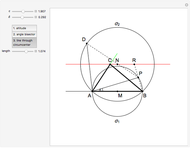
This Demonstration constructs a triangle  given the length
given the length  of its base
of its base 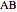 , the angle
, the angle  at the point
at the point  , and the length of the angle bisector at
, and the length of the angle bisector at  . The Demonstration uses the conchoid of Nicomedes, which is shown in red.
. The Demonstration uses the conchoid of Nicomedes, which is shown in red.
Contributed by: Izidor Hafner (October 2017)
Open content licensed under CC BY-NC-SA
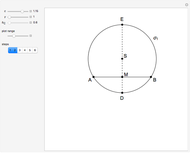
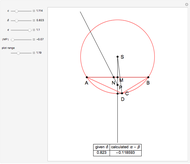
Snapshots
Details
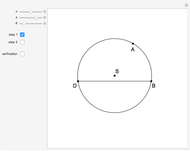
The base of a conchoid is a straight line 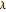 . Let
. Let 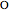 (the pole of the conchoid) be a point not on the base such that the distance of
(the pole of the conchoid) be a point not on the base such that the distance of 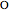 from
from 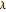 is
is  . Let
. Let  be a ray from
be a ray from 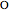 not parallel to the base. The ray
not parallel to the base. The ray  intersects the base at a point
intersects the base at a point 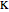 . Measure out points
. Measure out points  and
and 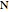 on the ray so that
on the ray so that  , where
, where  is a positive number. The conchoid determined by the base, the pole and
is a positive number. The conchoid determined by the base, the pole and  is the set of all such points
is the set of all such points  and
and 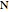 .
.
Permanent Citation