Freese's Dissection of a Regular Dodecagon into Six Squares

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
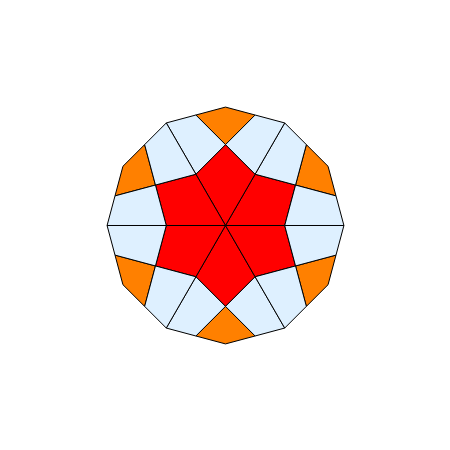
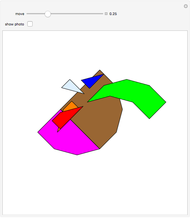
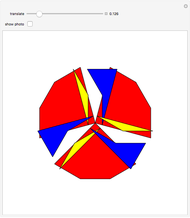
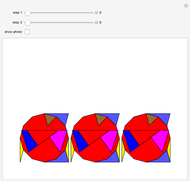
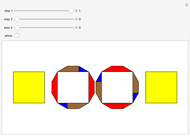
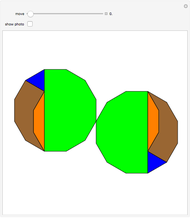
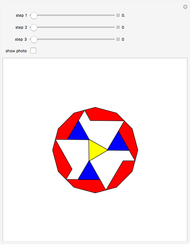
This Demonstration shows Freese's dissection of a regular dodecagon into six equal squares.
Contributed by: Izidor Hafner (May 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This dissection is described in [1, plate 126].
Reference
[1] G. N. Frederickson, Ernest Irving Freese's Geometric Transformations: The Man, the Manuscript, the Magnificent Dissections!, New Jersey: World Scientific, 2018.
Permanent Citation
"Freese's Dissection of a Regular Dodecagon into Six Squares"
http://demonstrations.wolfram.com/FreesesDissectionOfARegularDodecagonIntoSixSquares/
Wolfram Demonstrations Project
Published: May 17 2018