Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

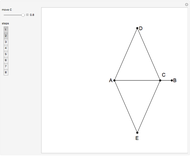
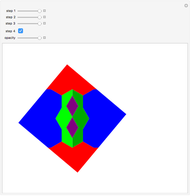
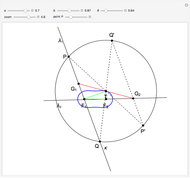
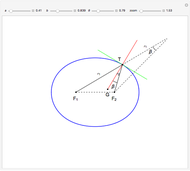
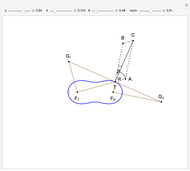
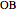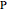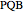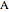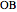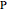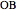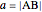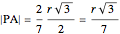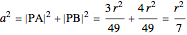A Construction of the Square Root of Seven

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

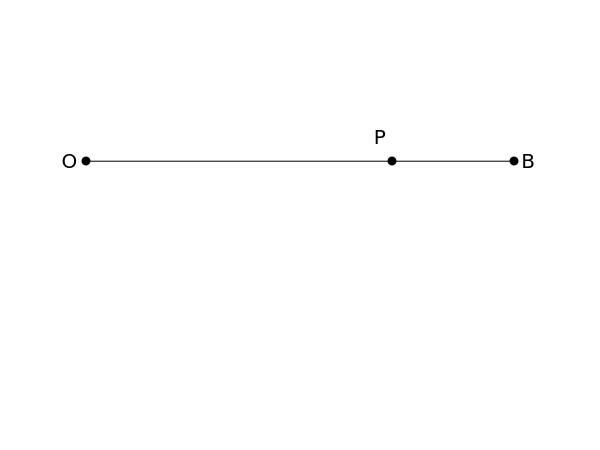
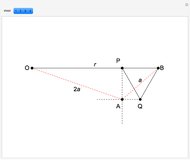
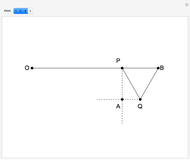
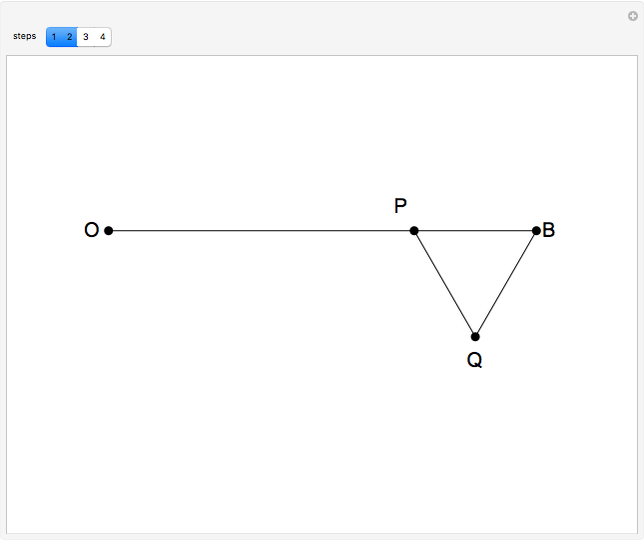
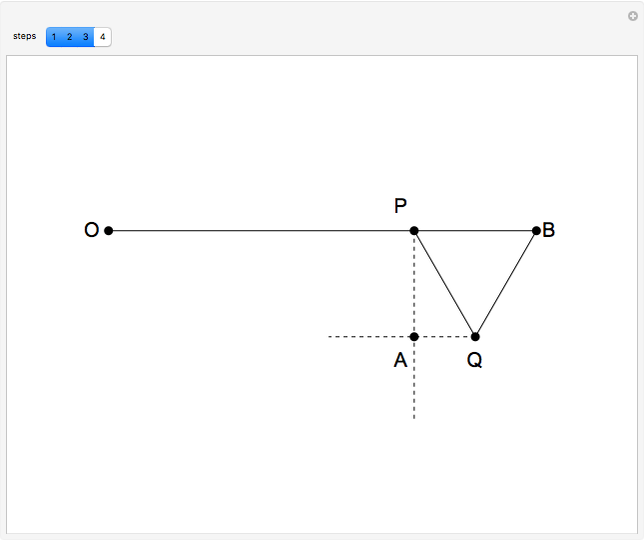
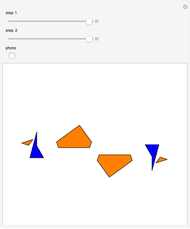
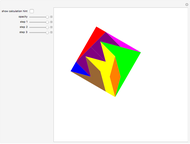
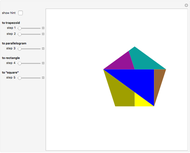
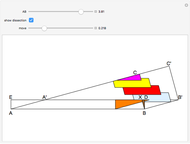
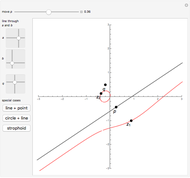
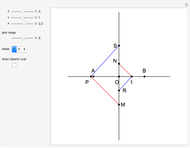
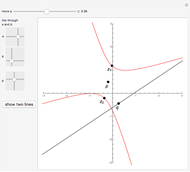
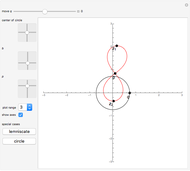
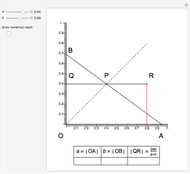
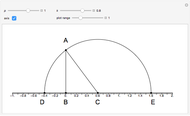
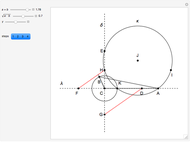
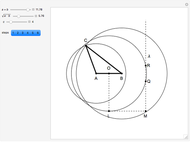
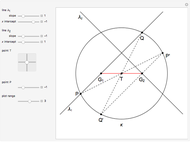
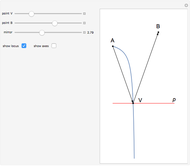
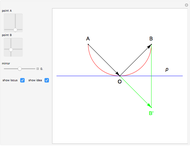
This Demonstration shows a construction of and such that .

[more]

Construction

Step 1: Draw a segment of length . Divide it by a point giving the ratio .

Step 2: Draw an equilateral triangle .

Step 3: Let be the intersection of the line through that is parallel to and the line through that is perpendicular to .

Step 4: Let . Then and have the required property.

Verification

.

Thus

.

[less]

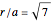Contributed by: Marko Razpet and Izidor Hafner (June 2018)
Open content licensed under CC BY-NC-SA

Details

The ratio appears in Pappus's hexagons problem.

References

[1] T. Heath, A History of Greek Mathematics, Volume II: From Aristarchus to Diophantus, New York: Dover Publications, 1981.

[2] A. Ostermann and G. Wanner, Geometry by Its History, New York: Springer, 2012.

Snapshots

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send