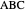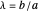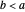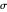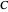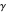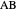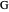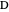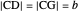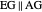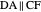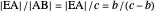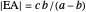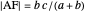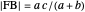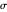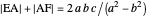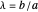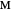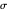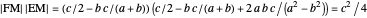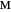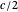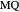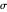The Apollonius Circle of a Triangle
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
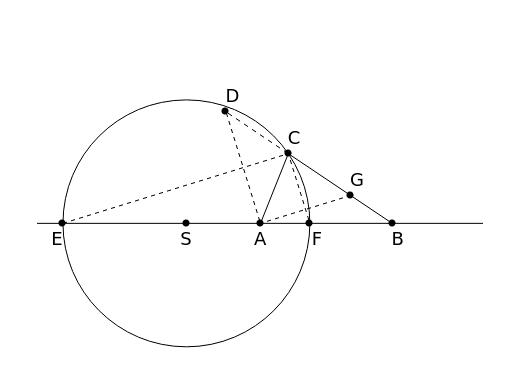
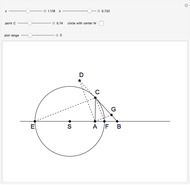
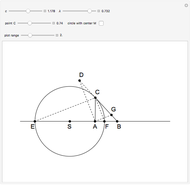
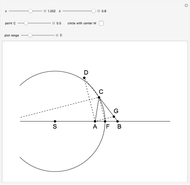
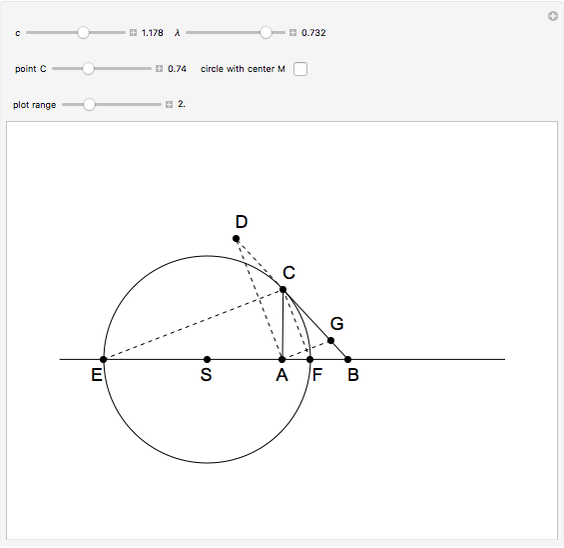
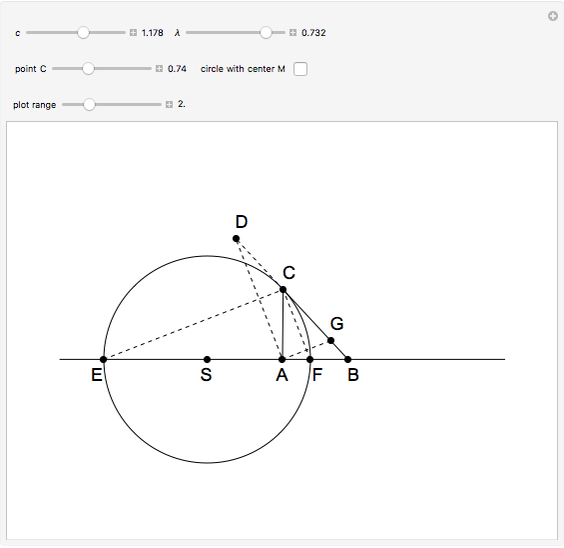
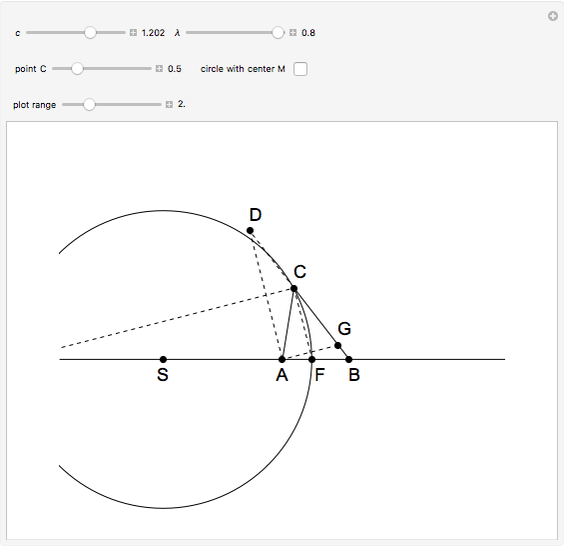
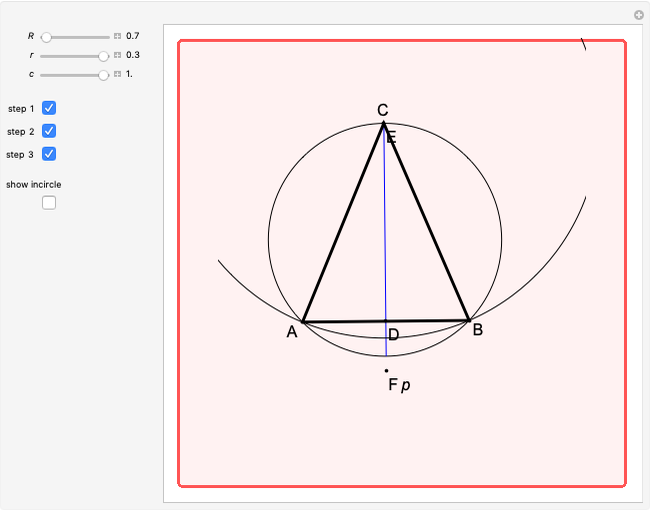
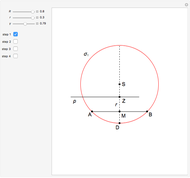
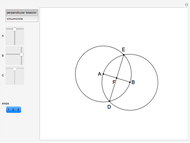
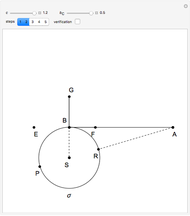
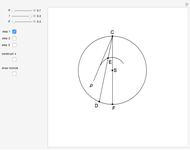
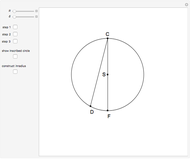
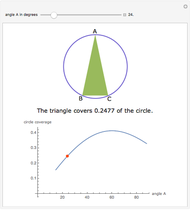
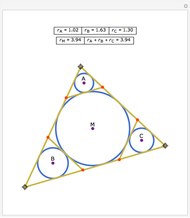
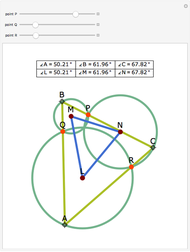
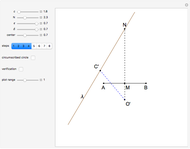
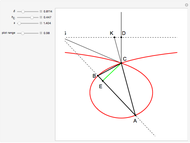
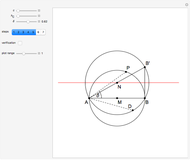
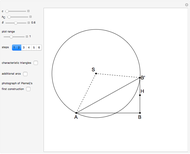
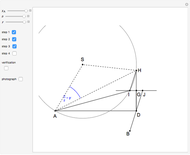
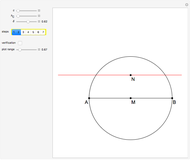
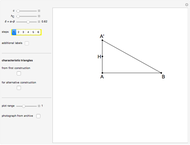
An Apollonius circle  is the locus of the apex of a triangle on a given base, the other two sides of which are in a fixed ratio.
is the locus of the apex of a triangle on a given base, the other two sides of which are in a fixed ratio.
Contributed by: Gerd Baron, Izidor Hafner, Marko Razpet and Nada Razpet (May 2018)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] E. J. Borowski and J. M. Borwein, Collins Dictionary of Mathematics, New York: HarperCollins Publishers, 1989 pp. 211–122.
Permanent Citation