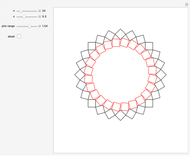
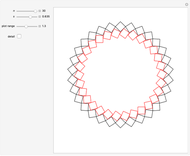
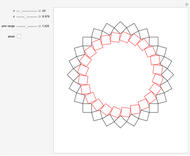
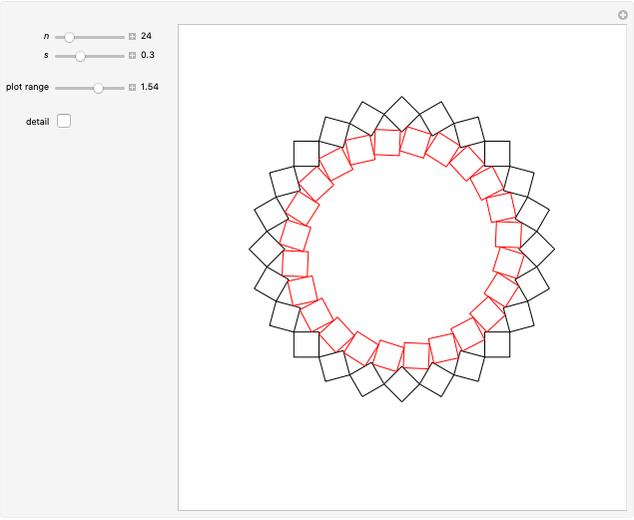
2. Families of Four-Point Touching Squares
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
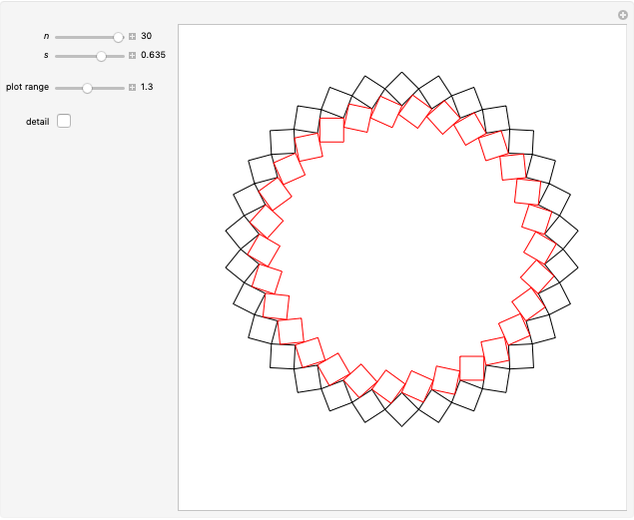
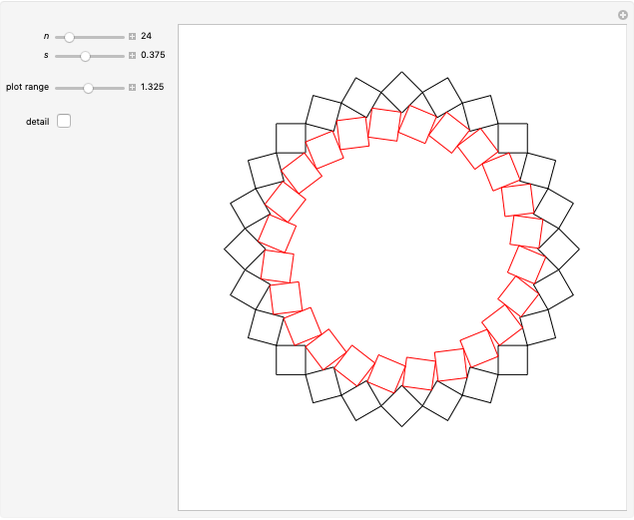
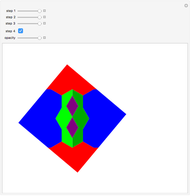
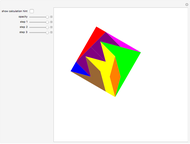
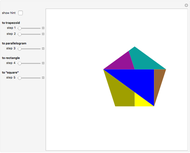
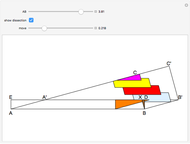
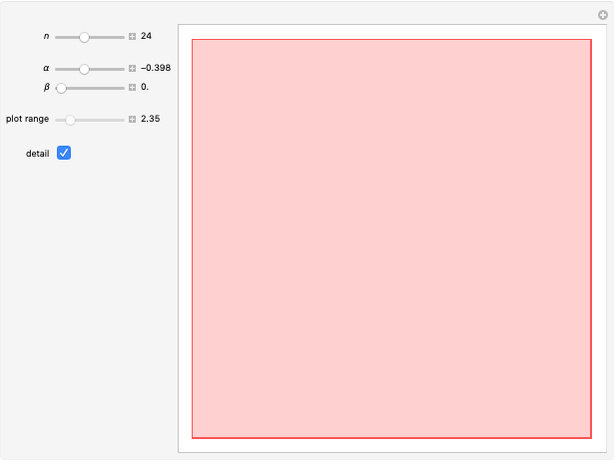
This Demonstration shows four-point touching families of 
squares, where 
. The parameter 
determines the point 
by 
, where 
is the radius vector of a point 
.
This generalizes [1], where 
. In this Demonstration you can vary 
within an appropriate range to maintain four-point touching in a family with 
.
Contributed by: Izidor Hafner (May 2019)
Open content licensed under CC BY-NC-SA
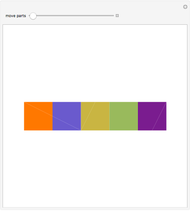
Snapshots
Details
A family 
is said to be 
-touching provided each element of 
has a nonempty intersection with precisely 
other elements of 
. A 
-touching family 
is said to be point-
-touching if any two touching sets have only a single common point [2].
Grünbaum has shown that example 
(with dihedral symmetry) in [3] is impossible. He has also said that it is not clear whether there are any point-4-touching families with fewer than 48 squares.
References
[1] I. Hafner. "Families of Four-Point Touching Squares" from the Wolfram Demonstrations Project—A Wolfram Web Resource. demonstrations.wolfram.com/FamiliesOfFourPointTouchingSquares.
[2] B. Grünbaum, "Families of Point-Touching Squares," Geombinatorics, 12(4), 2003 pp. 167–174. (Mar 27, 2019) sites.math.washington.edu/~grunbaum/Familiesofpointtouchin.pdf.
[3] E. Friedman, "Squares Touching a Constant Number of Other Squares," Geombinatorics, 12(2), 2002 pp. 55–60.
Permanent Citation
Constructing a Square with Sticks of Equal Length
Izidor Hafner
Decagon-to-Square Dissection
Izidor Hafner
Tilson's Square-to-Pentagram Dissection
Izidor Hafner
Dissecting a Dodecagram {12/2} to a Square
Izidor Hafner
Dissection of a Dodecagram {12/5} to a Square
Izidor Hafner
Dissection of a Pentagon to Almost a Square
Izidor Hafner
Tarski's Adaptation of Wojtowicz's Argument on Optimal Dissection of a Unit Square
Izidor Hafner
Families of Four-Point Touching Squares
Izidor Hafner
Hinged Dissections: From Three Squares to One
Jaime Rangel-Mondragon
Five-Squares-to-One Dissection
Izidor Hafner