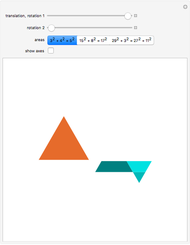
A Circle Defined from an Equilateral Triangle via Pythagoras

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
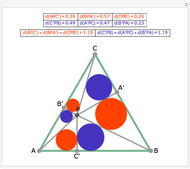
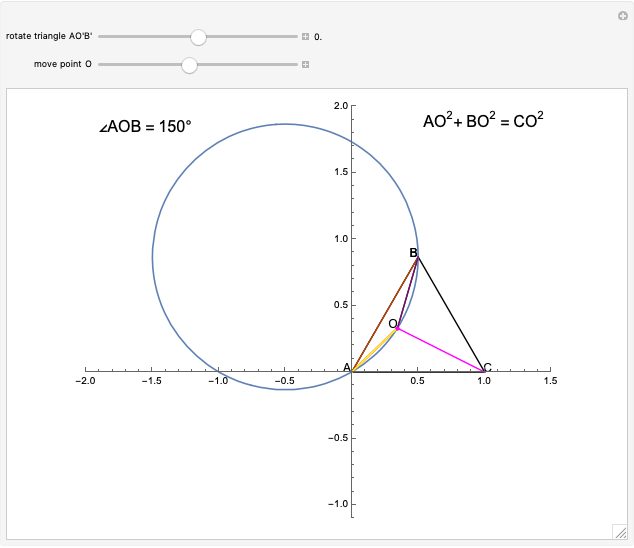
Consider an equilateral triangle 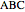 and the set of points
and the set of points 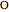 such that
such that 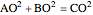 . Then
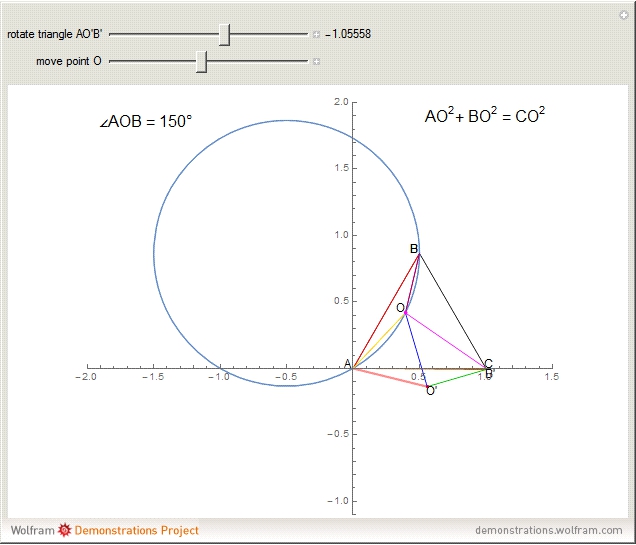
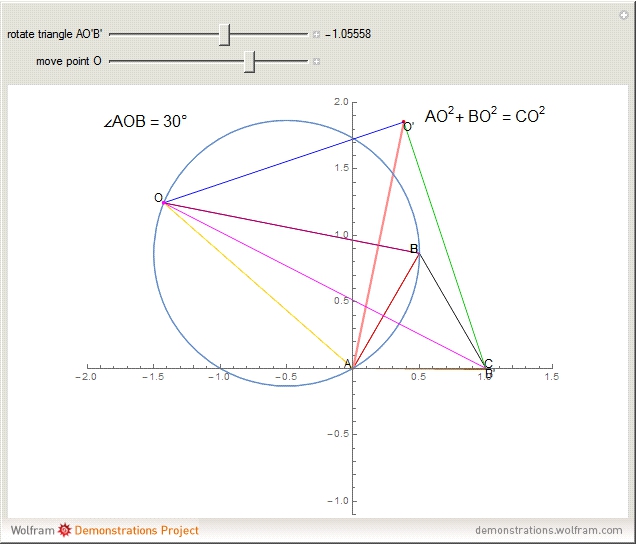
. Then 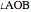 is either 30° or 150°, depending on whether
is either 30° or 150°, depending on whether  is inside or outside
is inside or outside 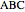 , and so the locus of
, and so the locus of  is a circle through
is a circle through 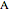 and
and 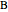 .
.
Contributed by: Dominic C. Milioto (September 2019)
Open content licensed under CC BY-NC-SA
Details
Use the "rotate" slider to rotate the triangle by 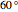 . This gives:
. This gives:
Snapshot 1: with 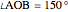
Snapshot 2: the point is outside the triangle with 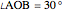
Snapshot 3: the point is at the top vertex of the triangle and 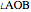 is undefined
is undefined
Proof [1]:
Suppose 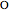 is inside the circle.
is inside the circle.
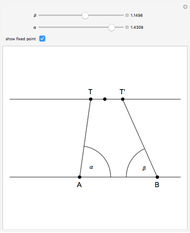
Rotate 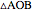 by
by 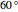 so that
so that 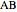 falls along
falls along 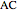 . Call the rotated triangle
. Call the rotated triangle 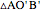 ; since
; since 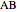 and
and 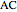 have equal lengths,
have equal lengths,  . Also, since
. Also, since 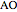 and
and  have equal lengths and
have equal lengths and 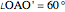 ,
, 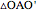 is equilateral and
is equilateral and 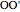 and
and 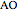 have equal lengths. Then:
have equal lengths. Then:
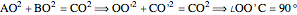 .
.
Since 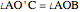 and
and  is equilateral,
is equilateral, 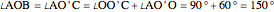 .
.
When 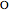 is outside
is outside  , a similar argument gives
, a similar argument gives 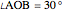 .
.
Reference
[1] AoPS Online. (Sep 10, 2019) artofproblemsolving.com/community/c3t48f3h1903996_geometry.
Snapshots
Permanent Citation