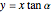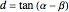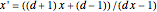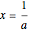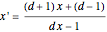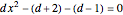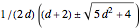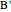The Plemelj Triangle via the Fixed Point of a Transformation

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
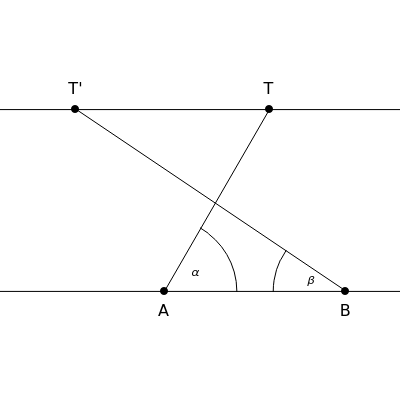
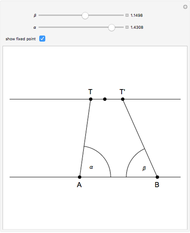
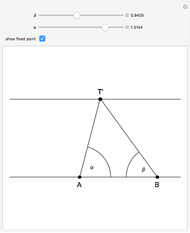
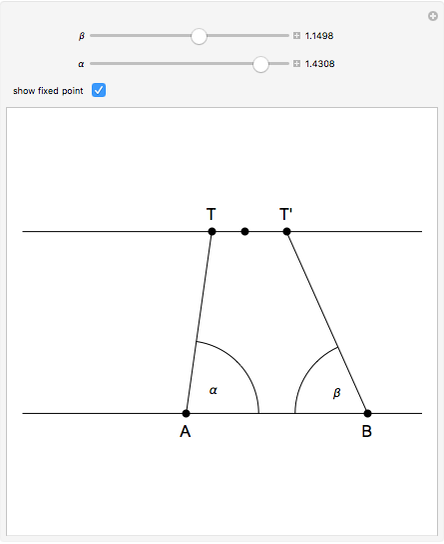
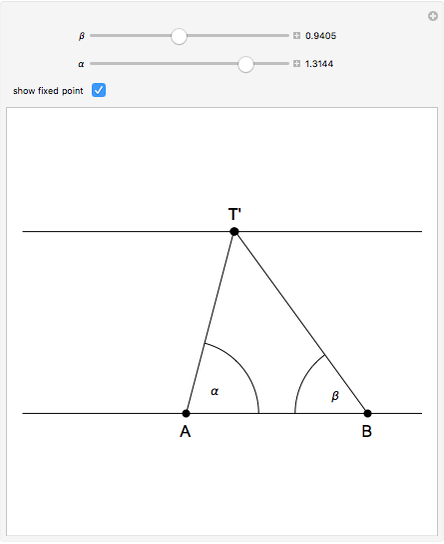
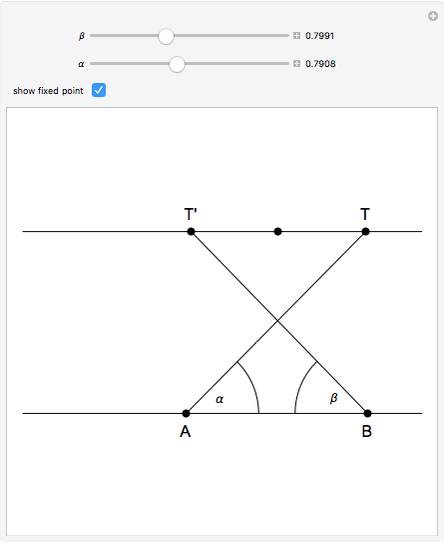
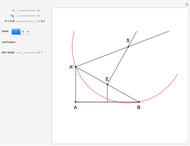
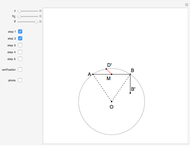
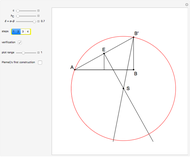
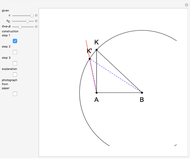
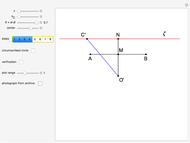
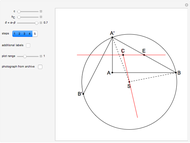
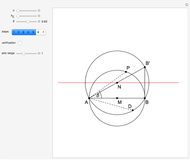
This problem was posed to Plemelj by his math teacher Borstner when Plemelj was about 16 years old. The problem asks for the construction of a triangle 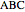 using ruler and compass given the length of the base
using ruler and compass given the length of the base 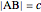 , the length of the altitude
, the length of the altitude  from
from  to
to  , and
, and  , where
, where  and
and 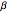 are the angles at
are the angles at 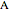 and
and 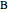 . In this Demonstration,
. In this Demonstration,  and
and 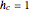 .
.
Contributed by: Izidor Hafner (June 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Plemelj (1873–1967) was Vidav's (1918–2015) dissertation adviser and later a professor at the University of Ljubljana.
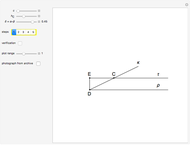
This Demonstration shows a way to solve the problem that Vidav mentioned to students of mathematics in 1952. The explanation here is based on [1].
Reference
[1] I. Pucelj, "Plemelj's Triangle and Fixed Points of Transformations," (in Slovenian), Obzornik za matematiko in fiziko, 62(1), 2015 pp. 12–14.
Permanent Citation