Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

A Discrete Model of Excitable Media

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

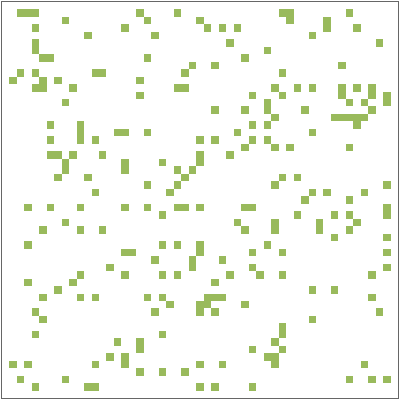
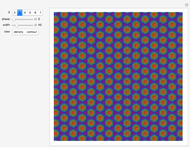
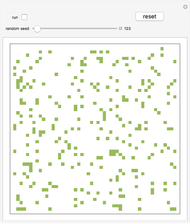
This Demonstration implements a model of excitable media. Space is represented as a grid of cells. Each cell can be in any of three states: (1) quiescent, (2) excited, or (3) refractory. A quiescent cell (white) becomes excited (green) if at least two of its neighbors are excited, then becomes refractory (yellow) at the next iteration. A refractory cell has a chance to become quiescent again with a fixed probability at every iteration.

Contributed by: Jeremy Owen (April 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Snapshot 1: the initial state of the model, which is mostly quiescent with randomly scattered excited cells

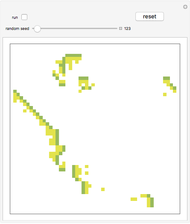
Snapshot 2: traveling waves emerging from disorder

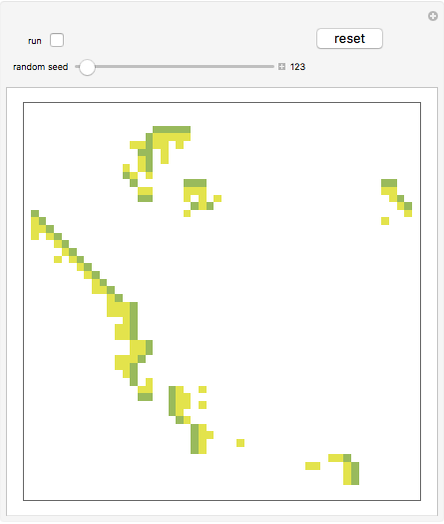
Snapshot 3: a very long, steplike, moving structure

The "reset" button at the top right returns the model to its initial state. When the "run" checkbox is checked, the model runs continuously. When it is unchecked, the model does not run. Boundary conditions are periodic.

Based on a model discussed in [1].

Reference

[1] J. L. Schiff, Cellular Automata: A Discrete View of the World, New York: Wiley, 2008.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send